
【题目】(2016湖北省荆州市第25题)阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.

问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
【答案】(1)、x=m,y=n,y=x+n﹣m,y=﹣x+m+n;(2)、y=![]() (x﹣2)2+3;(3)、
(x﹣2)2+3;(3)、![]() 或
或![]()
【解析】
试题分析:(1)、根据特征线直接求出点D的特征线;(2)、由点D的一条特征线和正方形的性质求出点D的坐标,从而求出抛物线解析式;(3)、分平行于x轴和y轴两种情况,由折叠的性质计算即可.
试题解析:(1)、∵点D(m,n), ∴点D(m,n)的特征线是x=m,y=n,y=x+n﹣m,y=﹣x+m+n;
(2)、点D有一条特征线是y=x+1, ∴n﹣m=1, ∴n=m+1
∵抛物线解析式为![]() , ∴y=
, ∴y=![]() (x﹣m)2+m+1,
(x﹣m)2+m+1,
∵四边形OABC是正方形,且D点为正方形的对称轴,D(m,n), ∴B(2m,2m),
∴![]() (2m﹣m)2+n=2m,将n=m+1带入得到m=2,n=3; ∴D(2,3), ∴抛物线解析式为y=
(2m﹣m)2+n=2m,将n=m+1带入得到m=2,n=3; ∴D(2,3), ∴抛物线解析式为y=![]() (x﹣2)2+3
(x﹣2)2+3
(3)、如图,当点A′在平行于y轴的D点的特征线时,

根据题意可得,D(2,3), ∴OA′=OA=4,OM=2, ∴∠A′OM=60°, ∴∠A′OP=∠AOP=30°,
∴MN=![]() =
=![]() , ∴抛物线需要向下平移的距离=3﹣
, ∴抛物线需要向下平移的距离=3﹣![]() =
=![]() .
.
当点A′在平行于x轴的D点的特征线时,
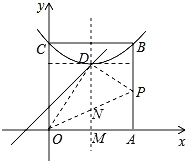
∵顶点落在OP上, ∴A′与D重合, ∴A′(2,3), 设P(4,c)(c>0),
由折叠有,PD=PA, ∴![]() =c, ∴c=
=c, ∴c=![]() , ∴P(4,
, ∴P(4,![]() ) ∴直线OP解析式为y=
) ∴直线OP解析式为y=![]() ,
,
∴N(2,![]() ), ∴抛物线需要向下平移的距离=3﹣
), ∴抛物线需要向下平移的距离=3﹣![]() =
=![]() ,
,
抛物线向下平移![]() 或
或![]() 距离,其顶点落在OP上.
距离,其顶点落在OP上.
考点(1)、折叠的性质;(2)、正方形的性质;(3)、特征线的理解


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016四川省乐山市第16题)在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若![]() ,则称点Q为点P的“可控变点”.
,则称点Q为点P的“可控变点”.
例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)若点(﹣1,﹣2)是一次函数![]() 图象上点M的“可控变点”,则点M的坐标为 ;
图象上点M的“可控变点”,则点M的坐标为 ;
(2)若点P在函数![]() (
(![]() )的图象上,其“可控变点”Q的纵坐标y′的取值范围是
)的图象上,其“可控变点”Q的纵坐标y′的取值范围是![]() ,则实数a的取值范围是 .
,则实数a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(提示:正方形的四条边都相等,四个角都是直角)
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为______,线段CF、BD的数量关系为______;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足 条件时,CF⊥BC(点C、F不重合),并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
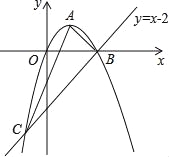
【题目】(2016广西省南宁市第24题)如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题

已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE.
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5条线段,它们的长度分别为1cm,2cm,3cm,4cm,5cm,以其中三条线段为边长,可组成不同的三角形的个数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com