
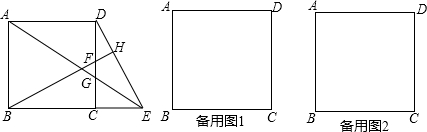
分析 (1)如图1,正方形ABCD中,AB=BC=DC,∠BCD=90°,因为BH⊥CD,得到∠CBF+∠DEB=90°,因为∠CDE+∠DEB=90°,得到△CBF≌△CDE,CF=CE,因为CD∥AB,所以$\frac{CE}{BC}=\frac{GE}{AG}$,所以$\frac{CF}{AB}=\frac{GE}{AG}$;(2))分两种情况:①当点F在线段DC上时,连接DQ,连接QG并延长交DE于点N.由△CQF∽△AQB得$\frac{CF}{AB}=\frac{QC}{AQ}$,∵$\frac{GF}{AB}=\frac{GE}{AG}$,
所以$\frac{GE}{AG}=\frac{QC}{AQ}$,由$\frac{GE}{AG}+1=\frac{QC}{AQ}+1$,得到$\frac{AE}{AG}=\frac{AC}{AQ}$,由三角形相似得到∠AQG=∠ACE,得到QG∥CE和△CQG为等腰直角三角形,
所以△CBQ≌△CDQ,因为∠CBQ=∠CDQ,∠CBQ=∠CDE,所以∠CDQ=∠CDE,再由DG=DG,∠DGQ=∠DGN=90°,得到△DQG≌△DNG,QG=GN,因为∠QHN=90°,
得到GH=QG,∠QHG=∠HQG=∠HBC,∠CPQ=∠GHQ+∠CED=∠HBC+∠CED=90°,
过点G作GM⊥GP交CP于点M,设PC与QG的交点为O,
由∠PQG+∠POQ=∠MCG+∠COG=90°,∠POQ=∠COG,得到∠PQG=∠MCG,同理∠PGQ=∠MGC,QG=CG所以△GPQ≌△GMC,PQ=CM,因为PM=$\sqrt{2}$PG,得到PC-PQ=PC-CM=PM=$\sqrt{2}$PG;
②当点F在线段DC延长线上时(如图3)连接DH并延长交QG的延长线于N,接下来思路和①相同.
解答 证明:(1)如图1,
正方形ABCD中,AB=BC=DC,∠BCD=90°
∵BH⊥CD,
∴∠BHE=90°,
∴∠CBF+∠DEB=90°,
又∵∠CDE+∠DEB=90°,
∴△CBF≌△CDE,
又∵∠CDE+∠DEB=90°,∴CF=CE,
∵CD∥AB,
∴$\frac{CE}{BC}=\frac{GE}{AG}$,
∴$\frac{CF}{AB}=\frac{GE}{AG}$;
(2)①当点F在线段DC上时 (如图2)
连接DQ,连接QG并延长交DE于点N.
由△CQF∽△AQB得$\frac{CF}{AB}=\frac{QC}{AQ}$,
∵$\frac{GF}{AB}=\frac{GE}{AG}$,
∴$\frac{GE}{AG}=\frac{QC}{AQ}$,
∴$\frac{GE}{AG}+1=\frac{QC}{AQ}+1$,
即$\frac{AE}{AG}=\frac{AC}{AQ}$,
又∵∠QAG=∠CAE,
∴△AQG∽△ACE,
∴∠AQG=∠ACE,
∴QG∥CE△CQG为等腰直角三角形,
∵$\left\{\begin{array}{l}{BC=CD}\\{∠BCQ=∠DCQ}\\{CQ=CQ}\end{array}\right.$,
∴△CBQ≌△CDQ,
∴∠CBQ=∠CDQ,
∵∠CBQ=∠CDE,
∴∠CDQ=∠CDE,
又∵DG=DG,∠DGQ=∠DGN=90°,
∴△DQG≌△DNG,
∴QG=GN,
又∵∠QHN=90°,
∴GH=QG,
∴∠QHG=∠HQG=∠HBC,
∴∠CPQ=∠GHQ+∠CED=∠HBC+∠CED=90°,
过点G作GM⊥GP交CP于点M,设PC与QG的交点为O,
∵∠PQG+∠POQ=∠MCG+∠COG=90°,∠POQ=∠COG,
∴∠PQG=∠MCG,
同理∠PGQ=∠MGC,
又∵QG=CG
∴△GPQ≌△GMC,
∴PQ=CM,
又∵PM=$\sqrt{2}$PG,
∴PC-PQ=PC-CM=PM=$\sqrt{2}$PG;
②当点F在线段DC延长线上时(如图3)
连接DH并延长交QG的延长线于N,由△CQF∽△AQB得$\frac{CF}{AB}=\frac{QC}{AQ}$,
∵$\frac{GF}{AB}=\frac{GE}{AG}$,
∴$\frac{GE}{AG}=\frac{QC}{AQ}$,
∴$\frac{GE}{AG}+1=\frac{QC}{AQ}+1$,
即$\frac{AE}{AG}=\frac{AC}{AQ}$,
又∵∠QAG=∠CAE,
∴△AQG∽△ACE,
∴∠AQG=∠ACE,
∴QG∥CE△CQG为等腰直角三角形,
∵$\left\{\begin{array}{l}{BC=CD}\\{∠BCQ=∠DCQ}\\{CQ=CQ}\end{array}\right.$,
∴△CBQ≌△CDQ,
∴∠CBQ=∠CDQ,
∵∠CBQ=∠CDE,
∴∠CDQ=∠CDE,
又∵DG=DG,∠DGQ=∠DGN=90°,
∴△DQG≌△DNG,
∴QG=GN,
又∵∠QHN=90°,
∴GH=QG,
∴∠QHG=∠HQG=∠HBC,
∴∠CPQ=∠GHQ+∠CED=∠HBC+∠CED=90°,
过点G作GM⊥GP交CP于点M,设PQ与CG的交点为O,
∵∠PQG+∠POQ=∠MCG+∠COG=90°,∠POQ=∠COG,
∴∠PQG=∠MCG,
同理∠PGQ=∠MGC,
又∵QG=CG
∴△GPQ≌△GMC,
∴PQ=CM,
又∵PM=$\sqrt{2}$PG,
PQ-PC=$\sqrt{2}$PG.
点评 本题主要考查了正方形的性质,等腰直角三角形的性质,三角形相似的判定和性质,三角形全等的判定和性质,特别是正确的做出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
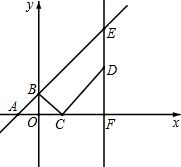 如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于点A,B.点C的坐标为(m,0),将线段BC绕点C顺时针旋转90°,并延长一倍得CD,过点D作x轴的垂线,垂足为F,交直线AB于点E.
如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于点A,B.点C的坐标为(m,0),将线段BC绕点C顺时针旋转90°,并延长一倍得CD,过点D作x轴的垂线,垂足为F,交直线AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+$\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2-$\frac{\sqrt{2}}{2}$ | D. | -$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com