
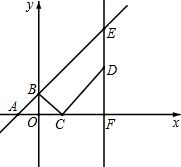
 如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于点A,B.点C的坐标为(m,0),将线段BC绕点C顺时针旋转90°,并延长一倍得CD,过点D作x轴的垂线,垂足为F,交直线AB于点E.
如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于点A,B.点C的坐标为(m,0),将线段BC绕点C顺时针旋转90°,并延长一倍得CD,过点D作x轴的垂线,垂足为F,交直线AB于点E.分析 (1)由在y=x+2中,令x=0得y=2,y=0得x=-2,得到OA=2,OB=2,△AOB是等腰直角三角形,再有DF⊥OC,得到△BOC∽△CFD,得比例式求解;
(2)由(1)知△BOC∽△CFD,再根据题意得:EF∥OB,于是得到△AFE是等腰直角三角形,根据AF=EF,求得DE,由四边形CDEP是平行四边形,得到PC∥DE,CD∥PE,求得∠DCF=∠EAF=45°,∠OCB=45°,得到OC=OB=2,求出m=2,得到结果;
(3)由△COQ与△BDE相似知,△BDE为直角三角形,得到∠BDE=90°,再由三角形相似求得结果.
解答 解:如图1,在y=x+2中,令x=0得y=2,y=0得x=-2,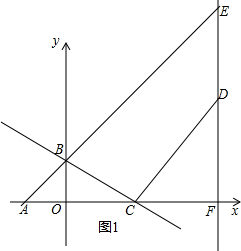
∴A(-2,0)B(0,2),即OA=2,OB=2,
∴∠OAB=∠OBA=45°,
(1)∵m=3,
∴OC=3,
∵∠BCD=90°,DF⊥OC,
得到△BOC∽△CFD,
∴$\frac{BC}{CD}$=$\frac{OC}{DF}$=$\frac{OB}{CF}$,
∵CD=2BC,
∴$\frac{3}{DF}$=$\frac{2}{CF}$=$\frac{1}{2}$,
∴CF=4,DF=6;
(2)如图1①∵OC=m,
由(1)知△BOC∽△CFD,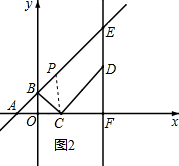
∴$\frac{m}{DF}$=$\frac{2}{CF}$=$\frac{1}{2}$,
根据题意得:EF∥OB,
∴△AFE是等腰直角三角形,
∴AF=EF,∴EF=m+6,
∴DE=6-m;
②第一种情况:如图2∵四边形PCDE是平行四边形,
∴PC∥DE,CD∥PE,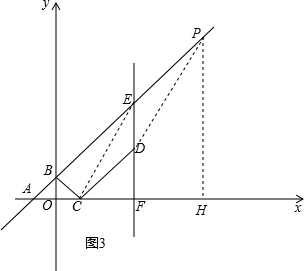
∴∠DCF=∠EAF=45°,
∴∠OCB=45°,
∴OC=OB=2,∴m=2,
∵点P在直线AB上,
∴P(2,4),
第二种情况:如图3,过点P作PH⊥AF于H,
当CE∥PD,CD∥PE,
∴∠DCF=45°=∠BCO,
∴m=2,CF=DF=4,EF=8,
∵PH=AH=12,
∴OH=10,
∴P(10,12);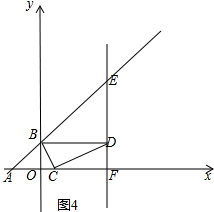
(3)如图4,∵△COQ与△BDE相似,
则△BDE为直角三角形,必有∠BDE=90°,
∴BD∥OF,
∴DF=OB=2,
∴OC=1,
∴m=1,
∵△BDE∽△COQ,
∴OQ=OC=1,
∵点Q在y轴上,
∴Q(1,0).
点评 本题主要考查了平面直角坐标系中求点的坐标,等腰直角三角形性质,相似三角形的判定和性质,平行四边形的判定和性质以及一次函数的综合应用,要注意的是(3)中,要根据P点的不同位置进行分类求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$+3$\sqrt{3}$=5$\sqrt{6}$ | B. | ($\sqrt{2}$+1)(1-$\sqrt{2}$)=1 | C. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{2}$ | D. | -(-a)4÷a2=a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com