
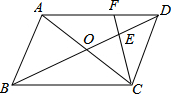
 如图,平行四边形ABCD中,对角线AC,BD相交于O,BC=18,E为OD中点,连结CE并延长交AD于F,则DF=8.
如图,平行四边形ABCD中,对角线AC,BD相交于O,BC=18,E为OD中点,连结CE并延长交AD于F,则DF=8. 分析 根据平行四边形的性质求出OD=OB,AD∥BC,推出△DEF∽△BEC,根据相似三角形的性质得出$\frac{DF}{BC}$=$\frac{DE}{BE}$,求出BE=3DE,即可求出答案.
解答 解:∵四边形ABCD是平行四边形,BC=18,
∴OD=OB,AD∥BC,
∴△DEF∽△BEC,
∴$\frac{DF}{BC}$=$\frac{DE}{BE}$,
∵E为OD中点,
∴DE=OE,
∵OD=OB,
∴BE=3DE,
∴BC=3DF,
∵BC=18,
∴DF=6.
故答案为:6.
点评 本题考查了平行四边形的性质,相似三角形的性质和判定的应用,能求出$\frac{DF}{BC}$=$\frac{DE}{BE}$和BE=3DE是解此题的关键,注意:平行四边形的对角线互相平分,平行四边形的对边互相平行.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 一班 | 二班 | 两班总和 | |
| 学生数 | x | y | 100 |
| 达标学生数 | 87.5%x | 75%y | 81%×100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
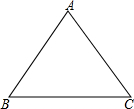 已知等边三角形ABC(如图).是否存在一点O,它到顶点A,B,C的距离相等,到边AB,AC,BC的距离也相等?如果有,请用圆规和直尺作出这个点,并说明理由;如果没有,请作出解释.
已知等边三角形ABC(如图).是否存在一点O,它到顶点A,B,C的距离相等,到边AB,AC,BC的距离也相等?如果有,请用圆规和直尺作出这个点,并说明理由;如果没有,请作出解释.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com