
【题目】如图,AB是⊙O 的直径,点D在⊙O 上(点D不与A,B重合),直线AD交过点B的切线于点C,过点D作⊙O 的切线DE交BC于点E.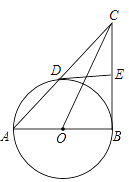
(1)求证:BE=CE;
(2)若DE平行AB,求sin∠ACO 的值.
【答案】(1)证明见解析;(2)sin∠ACO=![]() .
.
【解析】
(1)证明:连接OD,如图,利用切线长定理得到EB=ED,利用切线的性质得OD⊥DE,AB⊥CB,再根据等角的余角相等得到∠CDE=∠ACB,则EC=ED,从而得到BE=CE;
(2)作OH⊥AD于H,如图,设![]() 的半径为r,先证明四边形OBED为正方形得DE=CE=r,再利用△AOD和△CDE都为等腰直角三角形得到
的半径为r,先证明四边形OBED为正方形得DE=CE=r,再利用△AOD和△CDE都为等腰直角三角形得到![]() ,接着根据勾股定理计算出
,接着根据勾股定理计算出![]() ,然后根据正弦的定义求解.
,然后根据正弦的定义求解.
(1)证明:连接![]() ,如图,
,如图,
![]() 、
、![]() 为
为![]() 的切线,
的切线,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)解:作![]() 于
于![]() ,如图,设
,如图,设![]() 的半径为
的半径为![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为矩形,
为矩形,
而![]() ,
,
![]() 四边形
四边形![]() 为正方形,
为正方形,
![]() ,
,
易得![]() 和
和![]() 都为等腰直角三角形,
都为等腰直角三角形,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() 的值为
的值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点A(1,2),B(3,2),连接AB. 若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.
中,已知点A(1,2),B(3,2),连接AB. 若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.
(1)在点C(0,2),D(2,![]() ),E(4,1)中,线段AB的“临近点”是__________;
),E(4,1)中,线段AB的“临近点”是__________;
(2)若点M(m,n)在直线![]() 上,且是线段AB的“临近点”,求m的取值范围;
上,且是线段AB的“临近点”,求m的取值范围;
(3)若直线![]() 上存在线段AB的“临近点”,求b的取值范围.
上存在线段AB的“临近点”,求b的取值范围.
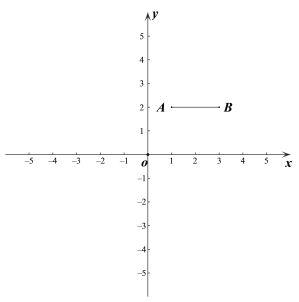
查看答案和解析>>
科目:初中数学 来源: 题型:
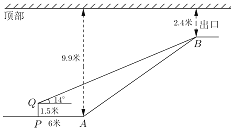
【题目】地铁10号线某站点出口横截面平面图如图所示,电梯![]() 的两端分别距顶部9.9米和2.4米,在距电梯起点
的两端分别距顶部9.9米和2.4米,在距电梯起点![]() 端6米的
端6米的![]() 处,用1.5米的测角仪测得电梯终端
处,用1.5米的测角仪测得电梯终端![]() 处的仰角为14°,求电梯
处的仰角为14°,求电梯![]() 的坡度与长度.(参考数据:
的坡度与长度.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
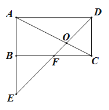
【题目】如图所示,在矩形ABCD中,点F是 BC的中点,DF的延长线与AB的延长线相交于点E,DE与AC相交于点O,若![]() ,则
,则![]() ( )
( )
A. 4 B. 6 C. 8 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
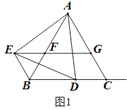
(1) 如图1,当点D在线段BC上时:
①求证:△AEB≌△ADC;②求证:四边形BCGE是平行四边形;
(2)如图2,当点D在BC的延长线上,且CD=BC时,试判断四边形BCGE是什么特殊的四边形?并说明理由.
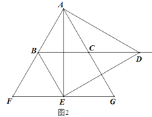
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象如下所示,下列5个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() (
(![]() 的实数),其中正确的结论有几个?
的实数),其中正确的结论有几个?
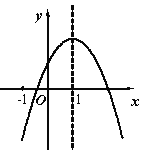
A. ①②③ B. ②③④ C. ②③⑤ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
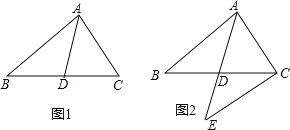
【题目】在△ABC中,D是边BC的中点.
(1)①如图1,求证:△ABD和△ACD的面积相等;
②如图2,延长AD至E,使DE=AD,连结CE,求证:AB=EC.
(2)当∠BAC=90°时,可以结合利用以上各题的结论,解决下列问题:
①求证:AD![]() BC(即:直角三角形斜边上的中线等于斜边的一半);
BC(即:直角三角形斜边上的中线等于斜边的一半);
②已知BC=4,将△ABD沿AD所在直线翻折,得到△ADB',若△ADB'与△ABC重合部分的面积等于△ABC面积的![]() ,请画出图形(草图)并求出AC的长度.
,请画出图形(草图)并求出AC的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com