
【题目】为了估计鱼塘中成品鱼(个体质量在0.5kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如表:
质量/kg | 0.5 | 0.6 | 0.7 | 1.0 | 1.2 | 1.6 | 1.9 |
数量/条 | 1 | 8 | 15 | 18 | 5 | 1 | 2 |
然后做上记号再放回水库中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
(1)请根据表中数据补全如图的直方图(各组中数据包括左端点不包括右端点). 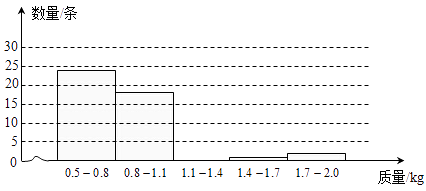
(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).
【答案】
(1)解:由函数图象可以得出1.1﹣1.4的有5条,补全图形,得:
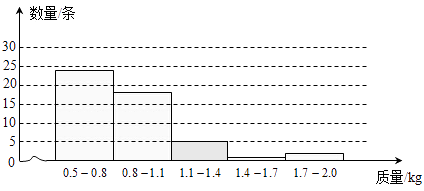
(2)解:由题意,得
0.5﹣0.8的频率为:24÷50=0.48,
0.8﹣1.1的频率为:18÷50=0.36,
1.1﹣1.4的频率为:5÷50=0.1,
1.4﹣1.7的频率为:1÷50=0.02,
1.7﹣2.0的频率为:2÷50=0.04.
∵0.48>0.36>0.1>0.04>0.02.
∴估计从鱼塘中随机捕一条成品鱼,其质量落在0.5﹣0.8的可能性最大
(3)解:这组数据的个数为50,就可以得出第25个和第26个数分别是1.0,1.0,
∴(1.0+1.0)÷2=1.0,
鱼塘里质量中等的成品鱼,其质量落在0.8﹣1.1内
(4)解:设鱼塘中成品鱼的条数为x,由题意,得:
50:x=2:100,
解得:x=2500.
2500× ![]() =2260kg
=2260kg
【解析】(1)由函数图象可以得出1.1﹣1.4的有5条,就可以补全直方图;(2)分别求出各组的频率,就可以得出结论;(3)由这组数据的个数为50,就可以得出第25个和第26个数的平均数就可以得出结论;(4)设鱼塘中成品鱼的条数为x,根据作记号的鱼50:x=2:100建立方程求出其解即可.
【考点精析】本题主要考查了频数分布直方图的相关知识点,需要掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE. 
(1)若AD=DB,OC=5,求切线AC的长;
(2)求证:ED是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程: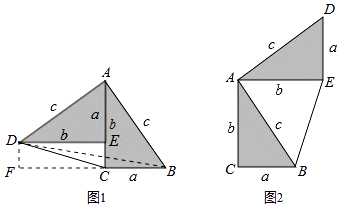
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2 .
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a.
∵S四边形ADCB=S△ACD+S△ABC= ![]() b2+
b2+ ![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB= ![]() c2+
c2+ ![]() a(b﹣a)
a(b﹣a)
∴ ![]() b2+
b2+ ![]() ab=
ab= ![]() c2+
c2+ ![]() a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2
证明:连结
∵S五边形ACBED=
又∵S五边形ACBED=
∴
∴a2+b2=c2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,连接BE,FE,则∠EBF的度数是( ) 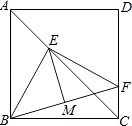
A.45°
B.50°
C.60°
D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
备用数据:tan60°=1.732,tan30°=0.577, ![]() =1.732,
=1.732, ![]() =1.414.
=1.414.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA= ![]() ,反比例函数y=
,反比例函数y= ![]() (k>0)的图象过CD的中点E.
(k>0)的图象过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,是判断点G是否在反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡AP的坡脚A处竖有一根电线杆AB,为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD,过点D作地面MN的垂线DH,H为垂足,已知点C、A、H在一直线上,若测得AC=7米,AD=12米,坡角为30° , 试求电线杆AB的高度;(精确到0.1米)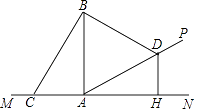
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com