
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() .
.
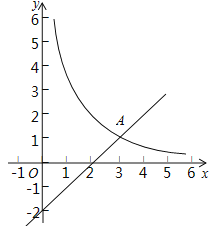
(1)求k、m的值;
(2)已知点![]() ,过点P作平行于x轴的直线,交直线
,过点P作平行于x轴的直线,交直线![]() 于点M,过点P作平行于y轴的直线,交函数
于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当![]() 时,判断线段PM与PN的数量关系,并说明理由;
时,判断线段PM与PN的数量关系,并说明理由;
②用含n的式子表示PN,则![]() ________.
________.
③若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.
【答案】(1)m=1,k=3;(2)①![]() ,理由见解析,②
,理由见解析,②![]() ,③
,③![]() 或
或![]() .
.
【解析】
(1)将A点代入![]() 中即可求出m的值,然后将A的坐标代入反比例函数中即可求出k的值;
中即可求出m的值,然后将A的坐标代入反比例函数中即可求出k的值;
(2)①当![]() 时,分别求出M、N两点的坐标即可求出PM与PN的关系;
时,分别求出M、N两点的坐标即可求出PM与PN的关系;
②由PN∥y轴,可用含n的代数式表示出点N的坐标,然后利用两点间的距离公式即可得出答案;
③由题意可求得点M的坐标,进而可得PM的长,由![]() ,再根据图象即可求出n的范围.
,再根据图象即可求出n的范围.
解:(1)将![]() 代入
代入![]() ,
,![]() ,
,![]() ,
,
将![]() 代入
代入![]() ,
,![]() ;
;
(2)①当![]() 时,
时,![]() ,如图,
,如图,
令![]() ,代入
,代入![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
令![]() ,代入
,代入![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
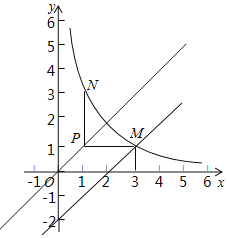
②∵![]() ,N(n,
,N(n,![]() ),∴PN=
),∴PN=![]() .
.
故答案为:![]() ;
;
③∵![]() ,∴点P在直线
,∴点P在直线![]() 上,
上,
过点P作平行于x轴的直线,交直线![]() 于点M,则
于点M,则![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
∴![]() ≥2,结合图象可得:
≥2,结合图象可得:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。
(1)求二次函数的解析式;
(2)设二次函数的图象与![]() 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线![]() ,并写出当
,并写出当![]() 在什么范围内时,一次函数的值大于二次函数的值。
在什么范围内时,一次函数的值大于二次函数的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2﹣2x+2﹣m=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)当m为何整数时,方程有两个不相等的整数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边落在坐标轴上,反比例函数y=![]() 的图象在第一象限的分支过AB的中点D交OB于点E,连接EC,若△OEC的面积为12,则k=_____.
的图象在第一象限的分支过AB的中点D交OB于点E,连接EC,若△OEC的面积为12,则k=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程mx2+(2m+1)x+m=0有两个实数根.
(1)求m的取值范围
(2)是否存在实数m,使方程的两实数根的倒数和为0?若存在,请求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,弦AB⊥AC,且AB=AC=6,点D在⊙O上,连接AD,BD,CD.
(1)如图1,若AD经过圆心O,求BD,CD的长;
(2)如图2,若∠BAD=2∠DAC,求BD,CD的长.
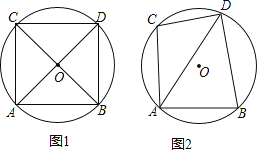
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:角的内部一点到角两边的距离比为1:2,这个点与角的顶点所连线段称为这个角的二分线.如图1,点P为∠AOB内一点,PA⊥OA于点A,PB⊥OB于点B,且PB=2PA,则线段OP是∠AOB的二分线.
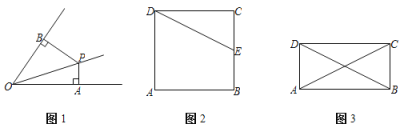
(1)图1中,OP为∠AOB的二分线,PB=4,PA=2,且OA+OB=8,求OP的长;
(2)如图2,正方形ABCD中,AB=2,点E是BC中点,证明:DE是∠ADC的二分线;
(3)如图3,四边形ABCD中,AB∥CD,∠ABC=90°,且∠CAB<∠CAD,∠BDC<∠BDA,若AC,BD分别是∠DAB,∠ADC的二分线,证明:四边形ABCD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
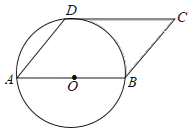
【题目】如图,ABCD中,∠DAB=45°,AB是⊙O的直径,点D在⊙O上,
(1)求证:CD是⊙O的切线;
(2)若AB=2,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com