
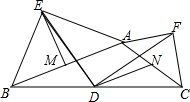
 如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=$\frac{1}{3}$S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )
如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=$\frac{1}{3}$S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①首先根据D是BC中点,N是AC中点N,可得DN是△ABC的中位线,判断出DN=$\frac{1}{2}AB$;然后判断出EM=$\frac{1}{2}AB$,即可判断出EM=DN;
②首先根据DN∥AB,可得△CDN∽ABC;然后根据DN=$\frac{1}{2}AB$,可得S△CDN=$\frac{1}{4}$S△ABC,所以S△CDN=$\frac{1}{3}$S四边形ABDN,据此判断即可.
③首先连接MD、FN,判断出DM=FN,∠EMD=∠DNF,然后根据全等三角形判定的方法,判断出△EMD≌△DNF,即可判断出DE=DF.
④首先判断出$\frac{EM}{EA}=sin45°=\frac{\sqrt{2}}{2}$,DM=$\frac{\sqrt{2}}{2}$FA,∠EMD=∠EAF,根据相似计三角形判定的方法,判断出△EMD∽△∠EAF,即可判断出∠MED=∠AEF,然后根据∠MED+∠AED=45°,判断出∠DEF=45°,再根据DE=DF,判断出∠DFE=45°,∠EDF=90°,即可判断出DE⊥DF.
解答 解:∵D是BC中点,N是AC中点,
∴DN是△ABC的中位线,
∴DN∥AB,且DN=$\frac{1}{2}AB$;
∵三角形ABE是等腰直角三角形,EM平分∠AEB交AB于点M,
∴M是AB的中点,
∴EM=$\frac{1}{2}AB$,
又∵DN=$\frac{1}{2}AB$,
∴EM=DN,
∴结论①正确;
∵DN∥AB,
∴△CDN∽ABC,
∵DN=$\frac{1}{2}AB$,
∴S△CDN=$\frac{1}{4}$S△ABC,
∴S△CDN=$\frac{1}{3}$S四边形ABDN,
∴结论②正确;
如图1,连接MD、FN,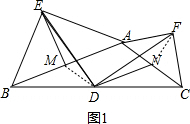 ,
,
∵D是BC中点,M是AB中点,
∴DM是△ABC的中位线,
∴DM∥AC,且DM=$\frac{1}{2}AC$;
∵三角形ACF是等腰直角三角形,N是AC的中点,
∴FN=$\frac{1}{2}AC$,
又∵DM=$\frac{1}{2}AC$,
∴DM=FN,
∵DM∥AC,DN∥AB,
∴四边形AMDN是平行四边形,
∴∠AMD=∠AND,
又∵∠EMA=∠FNA=90°,
∴∠EMD=∠DNF,
在△EMD和△DNF中,
$\left\{\begin{array}{l}{EM=DN}\\{∠EMD=∠DNF}\\{MD=NF}\end{array}\right.$,
∴△EMD≌△DNF,
∴DE=DF,
∴结论③正确;
如图2,连接MD,EF,NF,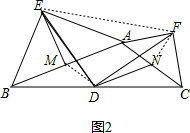 ,
,
∵三角形ABE是等腰直角三角形,EM平分∠AEB,
∴M是AB的中点,EM⊥AB,
∴EM=MA,∠EMA=90°,∠AEM=∠EAM=45°,
∴$\frac{EM}{EA}=sin45°=\frac{\sqrt{2}}{2}$,
∵D是BC中点,M是AB中点,
∴DM是△ABC的中位线,
∴DM∥AC,且DM=$\frac{1}{2}AC$;
∵三角形ACF是等腰直角三角形,N是AC的中点,
∴FN=$\frac{1}{2}AC$,∠FNA=90°,∠FAN=∠AFN=45°,
又∵DM=$\frac{1}{2}AC$,
∴DM=FN=$\frac{\sqrt{2}}{2}$FA,
∵∠EMD=∠EMA+∠AMD=90°+∠AMD,
∠EAF=360°-∠EAM-∠FAN-∠BAC
=360°-45°-45°-(180°-∠AMD)
=90°+∠AMD
∴∠EMD=∠EAF,
在△EMD和△∠EAF中,
$\left\{\begin{array}{l}{\frac{EM}{EA}=\frac{DM}{FA}=\frac{\sqrt{2}}{2}}\\{∠EMD=∠EAF}\end{array}\right.$
∴△EMD∽△∠EAF,
∴∠MED=∠AEF,
∵∠MED+∠AED=45°,
∴∠AED+∠AEF=45°,
即∠DEF=45°,
又∵DE=DF,
∴∠DFE=45°,
∴∠EDF=180°-45°-45°=90°,
∴DE⊥DF,
∴结论④正确.
∴正确的结论有4个:①②③④.
故选:D.
点评 (1)此题主要考查了全等三角形的判定和性质的应用,以及相似三角形的判定和性质的应用,要熟练掌握.
(2)此题还考查了等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.即:两个锐角都是45°,斜边上中线、角平分线、斜边上的高,三线合一,等腰直角三角形斜边上的高为外接圆的半径R,而高又为内切圆的直径.
(3)此题还考查了三角形中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.


科目:初中数学 来源: 题型:解答题
 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如下.
为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如下.| 分数段 | A | B | C | D | E | 合计 |
| 频数/人 | 12 | 36 | 84 | b | 48 | c |
| 频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 250 | 230 | … |
| B产品单价(元/件) | 130 | 120 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.
如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③$\widehat{BD}$=$\widehat{AD}$;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③$\widehat{BD}$=$\widehat{AD}$;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )| A. | ①② | B. | ①②③ | C. | ①④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
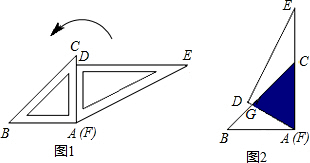 一副直角三角板按图1的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm.求两个三角形重叠部分(阴影)的面积(如图2).
一副直角三角板按图1的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm.求两个三角形重叠部分(阴影)的面积(如图2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
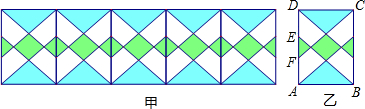
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com