
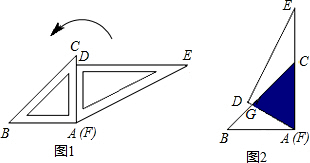 一副直角三角板按图1的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm.求两个三角形重叠部分(阴影)的面积(如图2).
一副直角三角板按图1的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm.求两个三角形重叠部分(阴影)的面积(如图2). 分析 过G点作GH⊥AC于H,由等腰直角三角形的性质得出GH=CH=$\frac{\sqrt{2}}{2}$CG=5$\sqrt{2}$cm,再由三角函数求出AH,得出AC,两个三角形重叠部分(阴影)的面积=$\frac{1}{2}$AC•GH,即可得出结果.
解答 解:过G点作GH⊥AC于H,如图所示: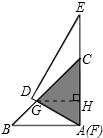
则∠GAC=60°,∠GCA=45°,GC=10cm,
在Rt△GCH中,GH=CH=$\frac{\sqrt{2}}{2}$CG=5$\sqrt{2}$cm,
在Rt△AGH中,AH=$\frac{\sqrt{3}}{3}$GH=$\frac{5\sqrt{6}}{3}$cm,
∴AC=CH+AH=(5$\sqrt{2}$+$\frac{5\sqrt{6}}{3}$)cm,
∴两个三角形重叠(阴影)部分的面积=$\frac{1}{2}$AC•GH=$\frac{1}{2}$×(5$\sqrt{2}$+$\frac{5\sqrt{6}}{3}$)×5$\sqrt{2}$=25+$\frac{25\sqrt{3}}{3}$(cm2).
点评 本题考查了旋转的性质、解直角三角形、三角形面积的计算;熟练掌握旋转的性质,并能进行推理计算是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
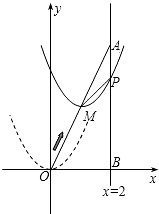 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
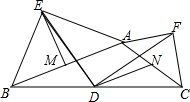 如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=$\frac{1}{3}$S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )
如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=$\frac{1}{3}$S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
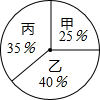 某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
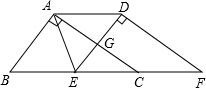 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论:
如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
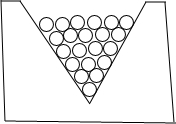 如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.
如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.| 最上层的产品数(支) | 1 | 2 | 3 | 4 | … | 10 | … |
| 产品总数 | 1 | 3 | 6 | 10 | … | 55 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
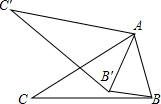 如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (6,20) | B. | (-6,20) | C. | (6,-20) | D. | (-6,-20) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com