
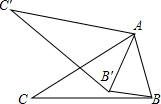
 如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
分析 由旋转的性质得出∠C′AB′=∠CAB=70°,AB′=AB,得出∠AB′B=∠ABB′,由平行线得出∠AB′B=∠C′AB′=70°,由三角形内角和求出∠BAB′,即可得出∠CAB′的度数.
解答 解:由旋转的性质得:∠C′AB′=∠CAB=70°,AB′=AB,
∴∠AB′B=∠ABB′,
∵BB′∥AC′,
∴∠AB′B=∠C′AB′=70°,
∴∠ABB′=70°,
∴∠BAB′=180°-70°-70°=40°,
∴∠CAB′=∠CAB-∠BAB′=70°-40°=30°;
故选:C.
点评 本题考查了旋转的性质、等腰三角形的性质、平行线的性质、三角形内角和定理;熟练掌握旋转的性质,并能进行推理计算是解决问题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:初中数学 来源: 题型:解答题
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 250 | 230 | … |
| B产品单价(元/件) | 130 | 120 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
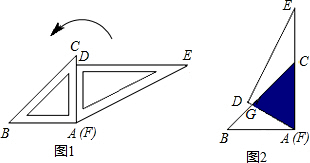 一副直角三角板按图1的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm.求两个三角形重叠部分(阴影)的面积(如图2).
一副直角三角板按图1的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm.求两个三角形重叠部分(阴影)的面积(如图2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向角是( )
如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向角是( )| A. | 西偏北30° | B. | 北偏西60° | C. | 北偏东30° | D. | 东偏北60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
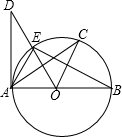 如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )
如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3-2=-1 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | a6÷a3=a3 | D. | (a+b)2=a2+b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com