

| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
分析 (1)根据图形发现火柴棒根数的增长规律计算填入表中即可;
(2)由表格可以看出火柴棒的递增规律,由此可得出火柴棒的根数的表达式;
(3)将n=100时代入(2)的表示式,即可得到火柴棒的根数;
(4)设火柴棒根数为s,将s=2013代入(2)的表达式,求n即可.
解答 解:(1)第4个图形火材棒的根数:1+4×2=9,第5个图形火材棒的根数:1+5×2=11;
故填:9;5.
(2)观察(1)中的表格,火柴棒根数以3为公差递增,故当三角形的个数为n时,火柴棒的根数为2n+1,
(3)当n=100时
2n+1=2×100+1=201;
即求当n=100时,火柴棒的根数是201根.
(4)设火柴棒根数为s,将s=2013代入(2)的表示式,即
2n+1=2013,解得,n=1006
故火柴棒的根数为2013时,三角形的个数是1006个.
点评 本题主要涉及图形的变化规律,难度中等.解决本题的关键是发现相邻图形的火柴棒根数的变化规律,注意由特殊到一般的归纳方法.


科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=( )
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
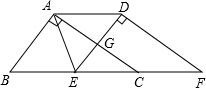 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论:
如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC方向平移2.5个单位得到△DEF,AC与DE相交于G点,连接AD,AE,则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
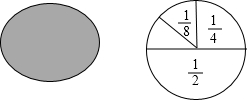 小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,…(如图所示):
小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,…(如图所示):查看答案和解析>>
科目:初中数学 来源: 题型:选择题
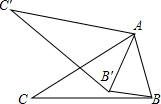 如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
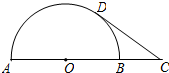 如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )
如图,AB是半圆的直径,点O是圆心,点C是AB延长线的一点,CD与半圆相切于点D.若AB=6,CD=4,则sin∠C的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
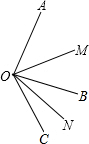 如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.
如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com