
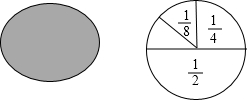
 小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,…(如图所示):
小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,…(如图所示):分析 (1)第1次剩1-$\frac{1}{2}$=$\frac{1}{2}$,第2次剩1-$\frac{1}{2}$-$\frac{1}{4}$=$\frac{1}{4}$,第3次剩1-$\frac{1}{2}$-$\frac{1}{4}$-$\frac{1}{8}$=$\frac{1}{8}$,…,第n次剩1-$\frac{1}{2}$-…-$\frac{1}{{2}^{n}}$=$\frac{1}{{2}^{n}}$,于是可以发现这张油饼切不完;
(2)由(1)的规律,把n=10,代入即可求出结果;
(3)由(1)知n次剩$\frac{1}{{2}^{n}}$,所以切了n次,一共将这张油饼切去了1-$\frac{1}{{2}^{n}}$.
解答 解:(1)由图形可以看出,第1次剩1-$\frac{1}{2}$=$\frac{1}{2}$,第2次剩1-$\frac{1}{2}$-$\frac{1}{4}$=$\frac{1}{4}$,第3次剩1-$\frac{1}{2}$-$\frac{1}{4}$-$\frac{1}{8}$=$\frac{1}{8}$,…,
第n次剩1-$\frac{1}{2}$-…-$\frac{1}{{2}^{n}}$=$\frac{1}{{2}^{n}}$,
所以这张油饼永远切不完;
(2)由(1)的规律,当n=10时,代入第n次剩的通式$\frac{1}{{2}^{n}}$,得出切了10次,那么剩下的油饼是整张油饼的$\frac{1}{{2}^{10}}$;
(3)由(1)知n次剩$\frac{1}{{2}^{n}}$,所以切了n次,一共将这张油饼切去了1-$\frac{1}{{2}^{n}}$.
点评 本题考查了根据图形探索规律问题,解决此类问题的关键是找出规律,发现问题的一般形式.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:选择题
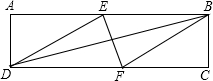 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:| A. | ①是真命题,②是真命题 | B. | ①是真命题,②是假命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①假命题,②假命题 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
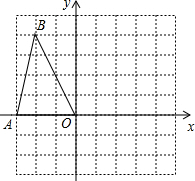 如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).
如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
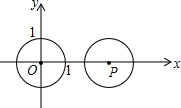 如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )
如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )| A. | 3 | B. | 1 | C. | 1,3 | D. | ±1,±3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com