
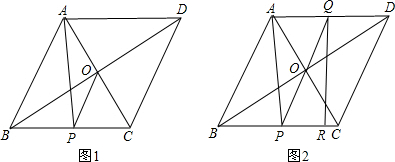
���� ��1�����öԳƵ����ʿɵ�AB=AD��BD=DC����AB=BC�ɵ�AB=BC=CD=DA���ó����ۣ�
��2�����������ε����ʵ�AC��BD��AO=OC=b��BO=OD�����ABC��BC���ϵĸ�Ϊh����y=S��AOP=$\frac{1}{2}{S}_{��ACP}$=$\frac{1}{2}��\frac{1}{2}��PC��h$=$\frac{1}{4}$��a-x��h������S��ABC=$\frac{1}{2}BC��h$=$\frac{1}{2}AC��OB$����h����y��x�仯�Ľ���ʽ��
��3����Rt��PQR�����Ϊs����y=sʱ�����ã�2���еĹ�ʽ�ɵ�PR=RC������OR����OA=OC��������λ�ߵ����ʿɵ�AP=2OR����Rt��PQR�У�б�ߵ����ߵ���б�ߵ�һ�룬�ɵ�PQ=2OR������AP=PQ��
��� �⣺��1���ı���ABCD�����Σ�
��D��B����ֱ��AC�ĶԳƵ㣬
��BD��AC��OB=OD��
��AB=AD��BC=DC
�֡�AB=BC��
��AB=BC=CD=DA��
���ı���ABCD�����Σ�
��2�����ı���ABCD�����Σ�
��AC��BD��AO=OC=b��BO=OD��
BP=x��AB=BC=a��
��PC=a-x��
���ABC��BC���ϵĸ�Ϊh��
��y=S��AOP=$\frac{1}{2}{S}_{��ACP}$=$\frac{1}{2}��\frac{1}{2}��PC��h$=$\frac{1}{4}$��a-x��h��
��Rt��AOB�У��ɹ��ɶ�����BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=$\sqrt{{a}^{2}-{b}^{2}}$��
����S��ABC=$\frac{1}{2}BC��h$=$\frac{1}{2}AC��OB$�ã�
h=$\frac{AC��OB}{BC}$=$\frac{2b\sqrt{{a}^{2}-{b}^{2}}}{a}$
��y=$\frac{1}{4}$��a-x��h=$\frac{b\sqrt{{a}^{2}-{b}^{2}}}{2a}$��a-x������0��x��a����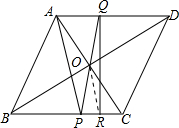
��3��PA=PQ��
��Rt��PQR�����Ϊs��y=s��
��y=$\frac{1}{4}$PC��h=s=$\frac{1}{2}PR��h$��
��PC=2PR��
��PR=RC��
����OR��OA=OC��
��AP=2OR��
��Rt��PQR�У�OΪб��PQ�е㣬
��PQ=2OR��
��AP=PQ��
���� ������Ҫ��������ԳƵ����ʣ����ε��ж����������ʶ����������ε������ʽ��ֱ�������ε����ʣ���������λ�ߵ����ʵȣ��ۺ����ø������������ε������ʽ�ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�У�MΪBC��һ�㣬F��AM���е㣬EF��AM������ΪF����AD���ӳ����ڵ�E����DC�ڵ�N��
��ͼ��������ABCD�У�MΪBC��һ�㣬F��AM���е㣬EF��AM������ΪF����AD���ӳ����ڵ�E����DC�ڵ�N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
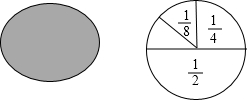 С÷�ڲ����Է�ʱ��������һ����Ȥ�����⣺��ʦϲ�������õ��ͱ����г�һ����С���Σ�С÷���룺�����һ����ȥԲ����һ�룬�ڶ�����ȥʣ���һ�룬�����μ�����ȥʣ���һ�룬������ͼ��ʾ����
С÷�ڲ����Է�ʱ��������һ����Ȥ�����⣺��ʦϲ�������õ��ͱ����г�һ����С���Σ�С÷���룺�����һ����ȥԲ����һ�룬�ڶ�����ȥʣ���һ�룬�����μ�����ȥʣ���һ�룬������ͼ��ʾ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 13cm | B�� | 11cm | C�� | 13cm����11cm | D�� | 8cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
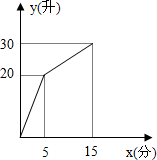 ij��ѧ����С������һ���н�ˮ�����ˮ�ܵ�����ģ��ˮ����ˮ�������ijʱ�̿�ʼ��5������ֻ��ˮ����ˮ��������10�����ڼȽ�ˮ�ֳ�ˮ��ÿ���ӵĽ�ˮ���ͳ�ˮ�������������������ڵ���ˮ��y����λ��L����ʱ��x����λ��min��֮��Ĺ�ϵ��ͼ��ʾ�����12���������ڵ���ˮ��Ϊ��������
ij��ѧ����С������һ���н�ˮ�����ˮ�ܵ�����ģ��ˮ����ˮ�������ijʱ�̿�ʼ��5������ֻ��ˮ����ˮ��������10�����ڼȽ�ˮ�ֳ�ˮ��ÿ���ӵĽ�ˮ���ͳ�ˮ�������������������ڵ���ˮ��y����λ��L����ʱ��x����λ��min��֮��Ĺ�ϵ��ͼ��ʾ�����12���������ڵ���ˮ��Ϊ��������| A�� | 22 | B�� | 25 | C�� | 27 | D�� | 28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com