
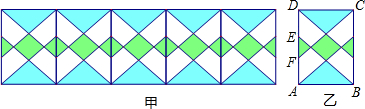
分析 首先取CD的中点G,连接HG,设AB=6acm,则BC=7acm,中间菱形的对角线HI的长度为xcm;然后根据GH∥BC,可得x=3.5a-2;再根据上下两个阴影三角形的面积之和为54cm2,可得a(7a-x)=18,据此求出a、x的值各是多少;最后根据AM∥FC,求出HK的长度,再用HK的长度乘以4,求出该菱形的周长为多少即可.
解答 解:如图乙,H是CF与DN的交点,取CD的中点G,连接HG,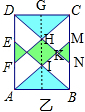 ,
,
设AB=6acm,则BC=7acm,中间菱形的对角线HI的长度为xcm,
∵BC=7acm,MN=EF=4cm,
∴CN=$\frac{7a+4}{2}$,
∵GH∥BC,
∴$\frac{GH}{CN}=\frac{DG}{DC}$,
∴$\frac{\frac{7a-x}{2}}{\frac{7a+4}{2}}=\frac{1}{2}$,
∴x=3.5a-2…(1);
∵上下两个阴影三角形的面积之和为54cm2,
∴6a•(7a-x)÷2=54,
∴a(7a-x)=18…(2);
由(1)(2),可得
a=2,x=5,
∴CD=6×2=12(cm),CN=$\frac{7a+4}{2}=\frac{7×2+4}{2}=9(cm)$,
∴DN=$\sqrt{{12}^{2}{+9}^{2}}$=15(cm),
又∵DH=$\sqrt{{DG}^{2}{+GH}^{2}}$=$\sqrt{{6}^{2}{+(\frac{7×2-5}{2})}^{2}}$=7.5(cm),
∴HN=15-7.5=7.5(cm),
∵AM∥FC,
∴$\frac{KN}{HK}=\frac{MN}{CM}$=$\frac{4}{9-4}=\frac{4}{5}$,
∴HK=$\frac{5}{4+5}×7.5=\frac{25}{6}(cm)$,
∴该菱形的周长为:
$\frac{25}{6}×4$=$\frac{50}{3}$(cm).
故答案为:$\frac{50}{3}$.
点评 (1)此题主要考查了菱形的性质和应用,要熟练掌握,解答此题的关键是要明确:①菱形具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.
(2)此题还考查了矩形的性质和应用,要熟练掌握,解答此题的关键是要明确:①平行四边形的性质矩形都具有;②角:矩形的四个角都是直角;③边:邻边垂直;
④对角线:矩形的对角线相等;⑤矩形是轴对称图形,又是中心对称图形.它有2条对称轴,分别是每组对边中点连线所在的直线;对称中心是两条对角线的交点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
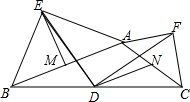 如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=$\frac{1}{3}$S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )
如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=$\frac{1}{3}$S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
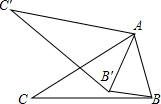 如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (6,20) | B. | (-6,20) | C. | (6,-20) | D. | (-6,-20) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
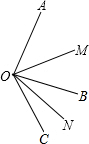 如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.
如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
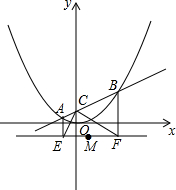 阅读理解
阅读理解查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com