
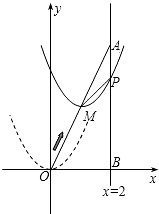
 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.分析 (Ⅰ)根据A点的坐标,用待定系数法即可求出直线OA的解析式.
(Ⅱ)①由于M点在直线OA上,可根据直线OA的解析式来表示出M点的坐标,因为M点是平移后抛物线的顶点,因此可用顶点式二次函数通式来设出这个二次函数的解析式,P的横坐标为2,将其代入抛物线的解析式中即可得出P点的坐标.
②PB的长,实际就是P点的纵坐标,因此可根据其纵坐标的表达式来求出PB最短时,对应的m的值.
(Ⅲ)根据(Ⅱ)中确定的m值可知:M、P点的坐标都已确定,因此AM的长为定值,若要使△QMA的面积与△PMA的面积相等,那么Q点到AM的距离和P到AM的距离应该相等,因此可分两种情况进行讨论:
①当Q在直线OA下方时,可过P作直线OA的平行线交y轴于C,那么平行线上的点到OA的距离可相等,因此Q点必落在直线PC上,可先求出直线PC的解析式,然后利用抛物线的解析式,看得出的方程是否有解,如果没有则说明不存在这样的Q点,如果有解,得出的x的值就是Q点的横坐标,可将其代入抛物线的解析式中得出Q点的坐标.
②当Q在直线OA上方时,同①类似,可先找出P关于A点的对称点D,过D作直线OA的平行线交y轴于E,那么直线DE上的点到AM的距离都等于点P到AM上的距离,然后按①的方法进行求解即可.
解答 解:(Ⅰ)设直线OA的解析式为y=kx,
把点A坐标(2,4)代入得,4=2k,
∴k=2,
∴直线OA的解析式为y=2x;
(Ⅱ)①∵顶点M的横坐标为m,且点M在直线OA上,
∴顶点M的坐标为(m,2m),
∴抛物线的解析式为y=(x-m)2+2m,
当x=2时,y=(2-m)2+2m=m2-2m+4(0≤x≤2),
∴点P的坐标为(2,m2-2m+4),
②PB=m2-2m+4=(m-1)2+3,
∵0≤x≤2,当m=1时,PB最短;
(Ⅲ)当PB最短时,抛物线的解析式为y=(x-1)2+2,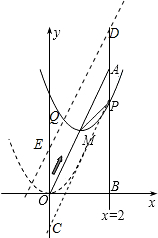
假设抛物线上存在点Q,使△QMA的面积与△PMA的面积相等,
设Q(x,x2-2x+3),
①当点Q在直线OA的下方时,过点P作直线PC∥AO,交y轴于点C,
∵PB=3,AB=4,
∴AP=1,
∴OC=1,
∴点C的坐标为(0,-1),
∵点P的坐标为(2,3),
∴直线PC的解析式为y=2x-1,
∵△QMA的面积与△PMA的面积相等,
∴点Q在直线PC上,
∴x2-2x+3=2x-1,解得x1=x2=2,即点Q(2,3),
∴与点P重合,所以这样的点Q不存在.
②当点Q落在直线OA的上方时,
作点P关于点A的对称称点D,过D作直线DE∥AO,交y轴于点E,
∵AP=1,
∴EO=DA=1,
∴E、D的坐标分别是(0,1),(2,5),
∴直线DE函数解析式为y=2x+1.
∵S△QMA=S△PMA,
∴点Q落在直线y=2x+1上.
∴x2-2x+3=2x+1.
解得:x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$.
代入y=2x+1得:y1=5+2$\sqrt{2}$,y2=5-2$\sqrt{2}$.
∴此时抛物线上存在点Q1(2+$\sqrt{2}$,5+2$\sqrt{2}$),Q2(2-$\sqrt{2}$,5-2$\sqrt{2}$)
使△QMA与△PMA的面积相等.
综上所述,抛物线上存在点,Q1(2+$\sqrt{2}$,5+2$\sqrt{2}$),Q2(2-$\sqrt{2}$,5-2$\sqrt{2}$)使△QMA与△PMA的面积相等.
点评 本题考查了一次函数解析式的确定、二次函数图象的平移、函数图象的交点、图形面积的求法等知识点,主要考查学生分类讨论和数形结合的数学思想方法.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如下.
为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如下.| 分数段 | A | B | C | D | E | 合计 |
| 频数/人 | 12 | 36 | 84 | b | 48 | c |
| 频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
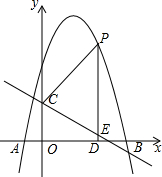 如图,抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(5,0),直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方抛物线上一个动点,过P作PE⊥x轴交直线CD于点E.设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(5,0),直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是x轴上方抛物线上一个动点,过P作PE⊥x轴交直线CD于点E.设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 250 | 230 | … |
| B产品单价(元/件) | 130 | 120 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.
如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
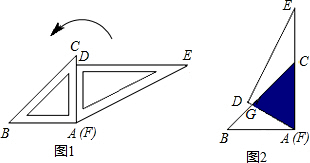 一副直角三角板按图1的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm.求两个三角形重叠部分(阴影)的面积(如图2).
一副直角三角板按图1的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm.求两个三角形重叠部分(阴影)的面积(如图2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com