
科目:初中数学 来源: 题型:选择题
| A. | 0.452×108 | B. | 4.52×107 | C. | 4.52×106 | D. | 4.52×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
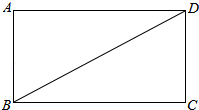 如图,BD是矩形ABCD的一条对角线.
如图,BD是矩形ABCD的一条对角线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a3)2=a5 | B. | ($\frac{1}{2}$a3b)2=$\frac{1}{4}$a6b2 | C. | (-x-y)2=x2-2xy+y2 | D. | (-a-b)(a+b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
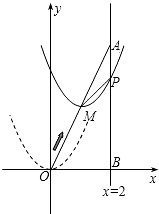 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
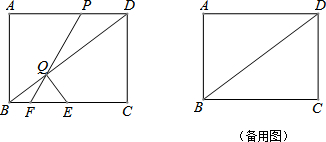
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
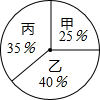 某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com