
【题目】已知,如图坐标平面内,A(﹣2,0),B(0,﹣4),AB⊥AC,AB=AC,△ABC经过平移后,得△A′B′C′,B点的对应点B′(6,0),A,C对应点分别为A′,C′.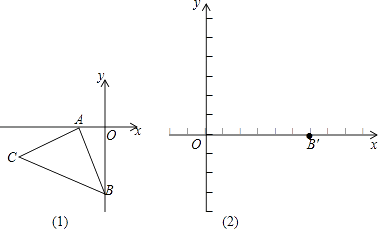
(1)求C点坐标;
(2)直接写出A′,C′坐标,并在图(2)中画出△A′B′C′;
(3)P为y轴负半轴一动点,以A′P为直角边以A’为直角顶点,在A′P右侧作等腰直角三角形A′PD.①试证明点D一定在x轴上;②若OP=3,求D点坐标.
【答案】
(1)
解:∵A(﹣2,0),B(0,﹣4),
∴AO=2,BO=4,
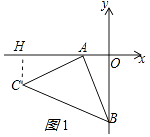
作CH⊥x轴于H,如图1所示:
则∠CHA=90°=∠AOB,
∴∠ACH+∠CAH=90°,
∵AB⊥AC,
∴∠BAO+∠CAH=90°,
∴∠ACH=∠BAO,
在△ACH和△BAO中, 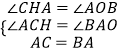 ,
,
∴△ACH≌△BAO(AAS),
∴AH=BO=4,CH=AO=2,
∴OH=AO+AH=6,
∴C(﹣6,﹣2)
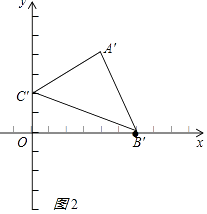
(2)
解:∵B(0,﹣4),B′(6,0),
∴△ABC向上平移4个单位长度,再向右平移6个单位长度,
∴A′(4,4),C′(0,2)
(3)
解:①连B′D,延长DB′交PC′于E,交A′P于F,如图3所示:
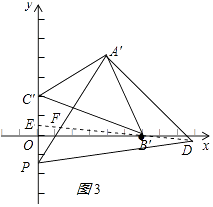
∵△A′B′C′和△A′PD是等腰直角三角形,
∴A′B′=A′C′,A′P=A′D,∠B′A′C′=∠DA′P=90°,
∴∠PA′C′=∠DA′B′,
在:△A′DB′和△A′PC′中, 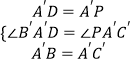 ,
,
∴△A′DB′≌△A′PC′(SAS),
∴∠A′DB′=∠A′PC′,
∵∠PFE=∠A′FD,
∴∠PEF=∠PA′D=90°,
∴DB′⊥y轴,
∴D点在x轴上;
②∵△A′DB′≌△A′PC′得,
∴B′D=C′P=5,
∴OD=11,
∴D(11,0).
【解析】(1)由点的坐标得出AO=2,BO=4,作CH⊥x轴于H,证出∠ACH=∠BAO,由AAS证明△ACH≌△BAO,得出AH=BO=4,CH=AO=2,求出OH=AO+AH=6,即可得出点C的坐标;C(﹣6,﹣2);(2)由B(0,﹣4)和B′(6,0),得出△ABC向上平移4个单位长度,再向右平移6个单位长度得△A′B′C′,即可得出A′,C′坐标,画出图形即可;(3)①连B′D,延长DB′交PC′于E,交A′P于F,由等腰直角三角形的性质得出A′B′=A′C′,A′P=A′D,∠B′A′C′=∠DA′P=90°,证出∠PA′C′=∠DA′B′,由SAS证明△A′DB′≌△A′PC′,得出∠A′DB′=∠A′PC′,由三角形内角和得出∠PEF=∠PA′D=90°,得出DB′⊥y轴,即可得出D点在x轴上;
②由全等三角形的性质得出B′D=C′P=5,得出OD=11,即可得出答案.


科目:初中数学 来源: 题型:
【题目】某公司在抗震救灾期间承担40 000顶救灾帐篷的生产任务,分为A、B、C、D四种型号,它们的数量百分比和每天单独生产各种型号帐篷的数量如图所示:
根据以上信息,下列判断错误的是( )
A.其中的D型帐篷占帐篷总数的10%
B.单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍
C.单独生产A型帐篷与单独生产D型帐篷的天数相等
D.单独生产B型帐篷的天数是单独生产A型帐篷天数的2倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:如图1,AB∥CD,∠PAB=140°,∠PCD=135°,求∠APC的度数.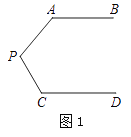
(1)丽丽同学看过图形后立即口答出:∠APC=85°,请你补全她的推理依据.
如图2,过点P作PE∥AB,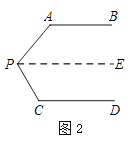
∵AB∥CD,∴PE∥CD. ()
∴∠A+∠APE=180°.
∠C+∠CPE=180°. ()
∵∠PAB=140°,∠PCD=135°,
∴∠APE=40°,∠CPE=45°
∴∠APC=∠APE+∠CPE=85°.()
问题迁移:
(2)如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α、∠β之间有何数量关系?请说明理由.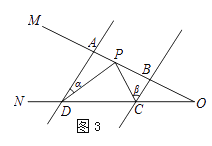
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与∠α、∠β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.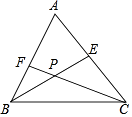
(1)若∠ABC=70°,∠ACB=50°,则∠BPC=°;
(2)求证:∠BPC=180°﹣ ![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画.要求每位同学必须参加,且限报一项活动.以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图.请你结合图示所给出的信息解答下列问题.
(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
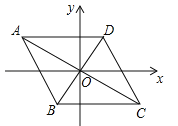
【题目】如图,已知点A(﹣4,2),B(﹣1,﹣2),平行四边形ABCD的对角线交于坐标原点O.
(1)请直接写出点C、D的坐标;
(2)写出从线段AB到线段CD的变换过程;
(3)直接写出平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
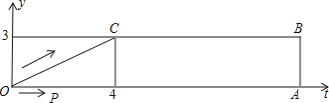
【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com