
����Ŀ�������龰����ͼ1��AB��CD����PAB=140�㣬��PCD=135�㣬���APC�Ķ�����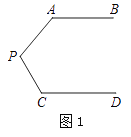
��1������ͬѧ����ͼ�κ������ڴ������APC=85�㣬���㲹ȫ�����������ݣ�
��ͼ2������P��PE��AB��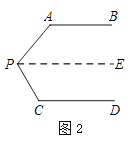
��AB��CD����PE��CD�� ����
���A+��APE=180�㣮
��C+��CPE=180�㣮 ����
�ߡ�PAB=140�㣬��PCD=135�㣬
���APE=40�㣬��CPE=45��
���APC=��APE+��CPE=85�㣮����
����Ǩ�ƣ�
��2����ͼ3��AD��BC������P��A��B����֮���˶�ʱ����ADP=�Ϧ�����BCP=�Ϧ£����CPD��Ϧ����Ϧ�֮���к�������ϵ����˵�����ɣ�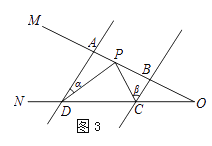
��3���ڣ�2���������£������P��A��B��������˶�ʱ����P���A��B��O���㲻�غϣ�������ֱ��д����CPD��Ϧ����Ϧ�֮���������ϵ��
���𰸡�
��1��ƽ����ͬһ��ֱ�ߵ�����ֱ��ƽ��,��ֱ��ƽ��,ͬ���ڽǻ���,��������
��2���⣺��CPD=�Ϧ�+�Ϧ£��������£�
��ͼ3��ʾ����P��PE��AD��CD��E��
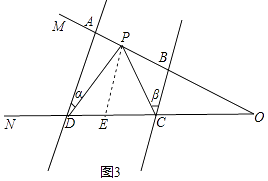
��AD��BC��
��AD��PE��BC��
��Ϧ�=��DPE���Ϧ�=��CPE��
���CPD=��DPE+��CPE=�Ϧ�+�Ϧ�
��3���⣺��P��BA�ӳ���ʱ����ͼ4��ʾ��
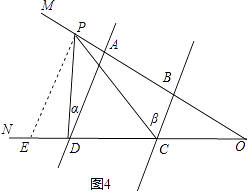
��P��PE��AD��CD��E��
ͬ��2����֪���Ϧ�=��DPE���Ϧ�=��CPE��
���CPD=�Ϧ©��Ϧ���
��P��AB�ӳ���ʱ����ͼ5��ʾ��
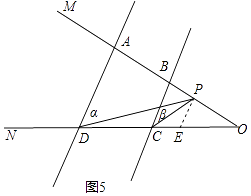
ͬ��2����֪���Ϧ�=��DPE���Ϧ�=��CPE��
���CPD=�Ϧ����Ϧ£�
����������1��ƽ����������߹���P��PE��AB��
��ͼ2��ʾ��
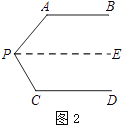
��AB��CD��
��PE��CD����ƽ����ͬһ��ֱ�ߵ�����ֱ��ƽ�У�
���A+��APE=180�㣮
��C+��CPE=180�㣮����ֱ��ƽ��ͬ���ڽǻ�����
�ߡ�PAB=130�㣬��PCD=120�㣬
���APE=50�㣬��CPE=60��
���APC=��APE+��CPE=110�㣮������������
���Դ��ǣ�ƽ����ͬһ��ֱ�ߵ�����ֱ��ƽ��|��ֱ��ƽ�У�ͬ���ڽǻ���|����������
��2����ȵ�1�⣬��ƽ����������۵㣬������ڴ��ǣ�ת���Ϧ����Ϧ£��ɵý���;
��3����ȵ�1�⣬��ƽ����������۵㣬������ڴ��ǣ�ת���Ϧ����Ϧ£���������ۣ��ɵý���.
�����㾫����������Ҫ������ƽ���ߵ��ж������ʵ����֪ʶ�㣬��Ҫ�����ɽǵ���Ȼ���������ϵ�����������õ�����ֱ��ƽ�У�λ�ù�ϵ������ƽ���ߵ��ж�����ƽ���ߣ�λ�ù�ϵ���õ��йؽ���Ȼ���������ϵ���Ľ�����ƽ���ߵ����ʲ�����ȷ�����⣮


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=��x+4����������ֱ��ཻ�ڵ�A��B���㣬��C���߶�AB������һ�㣬��C�ֱ���CD��x���ڵ�D��CE��y���ڵ�E��˫���� ![]() ��CD��CE�ֱ��ڵ�P��Q���㣬���ı���ODCEΪ�����Σ���
��CD��CE�ֱ��ڵ�P��Q���㣬���ı���ODCEΪ�����Σ��� ![]() ����k��ֵ�ǣ� ��
����k��ֵ�ǣ� ��
A.4
B.2
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������2.1ǧ��ѧУ�μӳ��������ᣬ��ѧУʱ�����ݳ��������ڼ��У���ʱ�������Ὺʼ����42���ӣ��������������ٲ��лؼң��ڼ��õ�������1���ӣ�Ȼ���������������г�����ѧУ����֪���������г���ѧУ������ѧУ���е�����ʱ��20���ӣ��������г����ٶ��Dz����ٶȵ�3����
��1���������е��ٶȣ���λ����/�֣��Ƕ��٣�
��2�������ܷ��������Ὺʼǰ�ϵ�ѧУ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.��a2?����a3��=a6
B.��a2����3=a��6
C.�� ![]() ����2=��a2��2a��1
����2=��a2��2a��1
D.��2a+1��0=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC�ա�AEF����F��BC�ϣ����н��ۣ� ��AC=AF �ڡ�FAB=��EAB �ۡ�FAC=��BAE ������C=50�㣬���BFE=80��
���������� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ���ڣ�A����2��0����B��0����4����AB��AC��AB=AC����ABC����ƽ�ƺá�A��B��C�䣬B��Ķ�Ӧ��B�䣨6��0����A��C��Ӧ��ֱ�ΪA�䣬C�䣮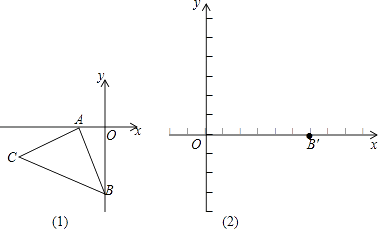
��1����C�����ꣻ
��2��ֱ��д��A�䣬C�����꣬����ͼ��2���л�����A��B��C�䣻
��3��PΪy�Ḻ����һ���㣬��A��PΪֱ�DZ���A��Ϊֱ�Ƕ��㣬��A��P�Ҳ�������ֱ��������A��PD������֤����Dһ����x���ϣ�����OP=3����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����E��CD���е㣬��ABD���ܳ�Ϊ16cm�����DOE���ܳ���cm�� 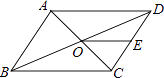
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com