
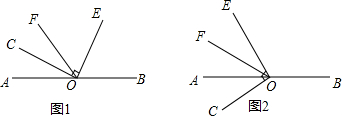
 如图,AB为⊙O的直径,P为AB延长线上一点,PC与⊙O相切于点C,∠P的平分线交BC、AC于点D、E.则下列结论不正确的是( )
如图,AB为⊙O的直径,P为AB延长线上一点,PC与⊙O相切于点C,∠P的平分线交BC、AC于点D、E.则下列结论不正确的是( )| A. | △PBC∽△PCA | B. | △PCD∽△PAE | ||
| C. | △CDE是等腰直角三角形 | D. | 点E、F三等分AC |
分析 根据两角对应相等的两个三角形相似的判定,即可证得A、B结论正确;根据△PCD∽△PAE,得出∠AEP=∠CDP,根据三角形外角的性质得出∠EFD=∠EDF,然后再根据圆周角定理证得∠ACB=90°,即可证得C结论正确;不能判断D结论.
解答 解:∵PC与⊙O相切于点C,
∴∠PCB=∠A,
∵∠BPC=∠CPA,
∴△PBC∽△PCA,故A结论正确;
∵∠PCB=∠A,∠APE=∠CPE,
∴△PCD∽△PAE,故B结论正确;
∵△PCD∽△PAE,
∴∠AEP=∠CDP,
∴∠EFD=∠EDF,
∴EC=DC,
∵AB是直径,
∴∠ACB=90°,
∴△CDE是等腰直角三角形,故C结论正确;
不能判断点E、F三等分AC,故D结论错误;
故选D.
点评 本题主要考查切线的性质、三角形相似的判定和性质、角平分线的性质、外角的性质、圆周角定理以及等腰三角形的判定,解题的关键熟练掌握性质定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
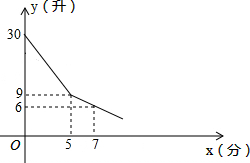 某校为学生装一台电开水器,课间操学生到开水器打水.假定每人水杯接水0.7升,他们先同时打开多个水笼头,后来因故障,关闭了故障水笼头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,开水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题.
某校为学生装一台电开水器,课间操学生到开水器打水.假定每人水杯接水0.7升,他们先同时打开多个水笼头,后来因故障,关闭了故障水笼头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,开水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com