Question

【题目】如图，已知抛物线与y轴交于点C（0，3），与x轴交于点A、B，点A在点B的左边，且B（3，0），AB=2

（1）求该抛物线的函数关系式；

（2）如果抛物线的对称轴上存在一点P，使得△APC的周长最小，求此时P点的坐标，并求出△APC周长；

（3）设D为抛物线上一点，E为对称轴上一点，若以点A、B、D、E为顶点的四边形是平行四边形，求点D的坐标．

Answer 1

【答案】(1) y=﹣4x+3 ；(2) 点P（2，1）时，△APC的周长最小，最小值为；(3) （0，3）或（4，3）或（2，﹣1）．

【解析】

试题分析：（1）先求出点A的坐标，根据两点式设出抛物线解析式，用待定系数法求出抛物线解析式；

（2）由点A，B关于抛物线对称轴对称，所以连接BC与抛物线对称轴的交点就是点P，根据两点间的距离公式求出各线段，即可；

（3）①AB为平行四边形的边时，就有AB∥DE，AB=DE，设出点D坐标，表示出点E坐标，由AB=DE求出点D坐标；

②AB为平行四边形的对角线时，AB，DE互相平分，而点E在抛物线对称轴上，得出点D也在抛物线对称轴上，即点D就是抛物线的顶点．

试题解析：（1）∵抛物线与x轴交于点A、B，点A在点B的左边，且B（3，0），AB=2，

∴A（1，0），

设抛物线解析式为y=a(x﹣1)(x﹣3)，

∵点C在抛物线上，

∴3=a×(﹣1)×(﹣3)=3a，

∴a=1，

∴抛物线解析式为y=(x﹣1)(x﹣3)=﹣4x+3，

（2）如图1，

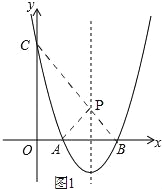
由（1）有，抛物线解析式为y=(x﹣1)(x﹣3)=﹣4x+3，

∴抛物线的对称轴为x=2，

连接BC，交对称轴于点P，连接AP，

∵点A与点B关于对称轴对称，

∴点P就是使得△APC的周长最小时，对称轴上的点，即：PA=PB，

∵B（3，0），C（0，3），

∴直线BC解析式为y=﹣x+3，BC=，

当x=2时，y=1，

∴P（2，1），

∵A（1，0），

∴AP=，

∴△APC周长=AC+AP+CP=AC+BC=+=，

即：点P（2，1）时，△APC的周长最小，最小值为；

（3）∵以点A、B、D、E为顶点的四边形是平行四边形，

∴分AB为对角线和边两种情况计算，

①当AB为平行四边形的边时，AB∥DE，AB=DE，

∵点D在抛物线上，

∴设点D（m，﹣4m+3），

∵点E在抛物线对称轴x=2上，

∴点E（2，﹣4m+3），

∵DE∥AB，

∴DE=|m﹣2|，

∵AB=DE，AB=2，

∴|m﹣2|=2，

∴m=0，或m=4，

∴D（0，3）或（4，3），

②当AB为平行四边形的对角线时，AB与DE互相平分，

∵点E在抛物线对称轴上，

∴点D也在抛物线的对称轴上，

即：点D就是抛物线的顶点，

由（1）得，抛物线解析式为y=（x﹣1）（x﹣3），

∴抛物线顶点坐标为（2，﹣1），

∴满足条件的点D的坐标为（0，3）或（4，3）或（2，﹣1）．