
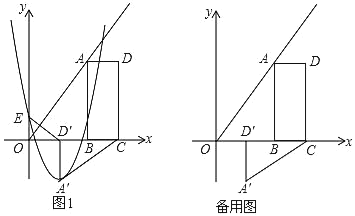
【题目】如图,B(2m,0)、C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线y=ax2+bx+n(a≠0)过E、A′两点.
(1)填空:∠AOB= °,用m表示点A′的坐标:A′ ;
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且![]() 时,△D′OE与△ABC是否相似?说明理由;
时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为M,过M作MN垂直y轴,垂足为N:
①求a、b、m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为5,请你探究a的取值范围.
【答案】(1)45;(m,﹣m);(2)△D′OE∽△ABC,理由见解析;(3)①b=﹣1﹣am;②![]() ≤a≤2.
≤a≤2.
【解析】
(1)由B与C的坐标求出OB与OC的长,根据OC-OB表示出BC的长,由题意AB=2BC,表示出AB,得到AB=OB,即三角形AOB为等腰直角三角形,即可求出所求角的度数;由旋转的性质得:OD′=D′A′=m,即可确定出A′坐标;
(2)△D′OE∽△ABC,理由如下:根据题意表示出A与B的坐标,由![]() ,表示出P坐标,由抛物线的顶点为A′,表示出抛物线解析式,把点E坐标代入整理得到m与n的关系式,利用两边对应成比例且夹角相等的三角形相似即可得证;
,表示出P坐标,由抛物线的顶点为A′,表示出抛物线解析式,把点E坐标代入整理得到m与n的关系式,利用两边对应成比例且夹角相等的三角形相似即可得证;
(3)①当E与原点重合时,把A与E坐标代入y=ax2+bx+c,整理即可得到a,b,m的关系式;
②抛物线与四边形ABCD有公共点,可得出抛物线过点C时的开口最大,过点A时的开口最小,分两种情况考虑:若抛物线过点C(3m,0),此时MN的最大值为5,求出此时a的值;若抛物线过点A(2m,2m),求出此时a的值,即可确定出抛物线与四边形ABCD有公共点时a的范围.
解:(1)∵B(2m,0),C(3m,0),∴OB=2m,OC=3m,即BC=m,
∵AB=2BC,
∴AB=2m=0B,
∵∠ABO=90°,
∴△ABO为等腰直角三角形,
∴∠AOB=45°,
由旋转的性质得:OD′=D′A′=m,即A′(m,﹣m);
故答案为:45;(m,﹣m);
(2)△D′OE∽△ABC,理由如下:
由已知得:A(2m,2m),B(2m,0),
∵![]() ,
,
∴P(2m,m),
∵A′为抛物线的顶点,
∴设抛物线解析式为y=a(x﹣m)2﹣m,
∵抛物线过点E(0,n),
∴n=a(0﹣m)2﹣m,即m=2n,
∴OE:OD′=BC:AB=1:2,
∵∠EOD′=∠ABC=90°,
∴△D′OE∽△ABC;
(3)①当点E与点O重合时,E(0,0),
∵抛物线y=ax2+bx+n过点E,A′,
∴![]() ,
,
整理得:am+b=﹣1,即b=﹣1﹣am;
②∵抛物线与四边形ABCD有公共点,
∴抛物线过点C时的开口最大,过点A时的开口最小,
若抛物线过点C(3m,0),此时MN的最大值为5,
∴a(3m)2﹣(1+am)3m=0,
整理得:am=![]() ,即抛物线解析式为y=
,即抛物线解析式为y=![]() ,
,
由A(2m,2m),可得直线OA解析式为y=x,
联立抛物线与直线OA解析式得: ,
,
解得:x=5m,y=5m,即M(5m,5m),
令5m=5,即m=1,
当m=1时,a=![]() ;
;
若抛物线过点A(2m,2m),则a(2m)2﹣(1+am)2m=2m,
解得:am=2,
∵m=1,
∴a=2,
则抛物线与四边形ABCD有公共点时a的范围为![]() ≤a≤2.
≤a≤2.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
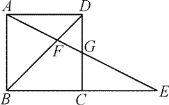
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
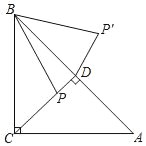
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
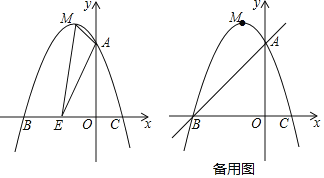
【题目】如图,抛物线y=ax2+bx+3交y轴于点A,交x轴于点B(-3,0)和点C(1,0),顶点为点M.
(1)求抛物线的解析式;
(2)如图,点E为x轴上一动点,若△AME的周长最小,请求出点E的坐标;
(3)点F为直线AB上一个动点,点P为抛物线上一个动点,若△BFP为等腰直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
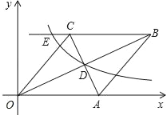
【题目】如图,在直角坐标系中有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=![]() (x>0)经过点D,交BC的延长线于点E,且OBAC=160,则点E的坐标为_____.
(x>0)经过点D,交BC的延长线于点E,且OBAC=160,则点E的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是长为10m,倾斜角为30°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).(参考数据:sin65°=0.90,tan65°=2.14)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22017
首先设S=1+2+22+23+24+…+22017 ① 则2S=2+22+23+24+25+…+22018 ②
②﹣①得S=22018﹣1 即1+2+22+23+24+…+22017=22018﹣1
以上解法,在数列求和中,我们称之为:“错位相减法”
请你根据上面的材料,解决下列问题
(1)求1+3+32+33+34+…+32019的值
(2)若a为正整数且![]() ,求
,求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
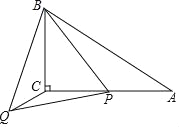
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+(m﹣1)x+m与y轴交于(0,3)点.
(1)求出m的值并画出这条抛物线;
(2)求它与x轴的交点和抛物线顶点的坐标;
(3)x取什么值时,抛物线在x轴上方?
(4)x取什么值时,y的值随x值的增大而减小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com