
ЁОЬтФПЁПШчЭМ1ЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAдкyжсе§АыжсЩЯЃЌЕуBЁЂCЗжБ№дкxжсЕФИКАыжсЁЂе§АыжсЩЯЃЌЧвABЃНACЃЌЁЯACBЃН30ЁуЃЌODЁЭABгкЕуDЃЎ
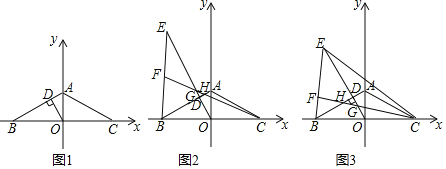
ЃЈ1ЃЉЧѓжЄЃКBDЃН3ADЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕуEдкODЕФбгГЄЯпЩЯЃЌСЌНгBEЃЌдкЯпЖЮBEЩЯШЁЕуFЃЌСЌНгCFЗжБ№НЛOEЁЂABгкЕуGЁЂHЃЈЕуGЁЂHЁЂDЛЅВЛжиКЯЃЉЃЌШєFEЃНFGЃЌЧѓжЄЃКЁЯEBAЉЁЯBCFЕФЖШЪ§ЮЊЖЈжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгECЃЌШєCЃЈ4![]() ЃЌ0ЃЉЃЌAЃЈ0ЃЌ4ЃЉЃЌЧѓSЁїECGЃЎ
ЃЌ0ЃЉЃЌAЃЈ0ЃЌ4ЃЉЃЌЧѓSЁїECGЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉSЁїEGCЃН12![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнжБНЧШ§НЧаЮжаЕФе§грЯвЖЈРэЃЌПЩЕУЕНBDгыADЕФГЄЖШЙиЯЕ.ЃЈ2ЃЉИљОнШ§НЧаЮЕФФкНЧКЭЙЋЪНЃЌПЩЕУЁЯEBAЉЁЯBCFЃН30Ёу.ЃЈ3ЃЉвдBЮЊдВаФЃЌBOГЄЮЊАыОЖЛЛЁНЛEDгкЕуMЃЌСЌНгBMЃЌЙ§ЕуCзїEOЕФДЙЯпЃЌНЛEOЕФбгГЄЯпгкЕуNЃЌдйИљОнШЋЕШШ§НЧаЮаджЪЃЌПЩЕУSЁїEGC.
НтЃКЃЈ1ЃЉЁпABЃНACЃЌЁЯACBЃН30ЁуЃЌODЁЭAB
ЁрЁЯABCЃН30ЁуЃЌЁЯODBЃН90ЁуЃЌ
ЁрЁЯBODЃН60ЁуЃЌ
ЁрЁЯAODЃН30ЁуЃЌ
ЁрADЃН![]() OAЃЌOAЃН
OAЃЌOAЃН![]() AB
AB
ЁрOAЃН2ADЃЌABЃН2AOЃЌ
ЁрABЃН4ADЃЌ
ЁрBDЃН3ADЃЎ
ЃЈ2ЃЉЁпFEЃНFGЃЌ
ЁрЩшЁЯEЃНЁЯEGFЃНІСЃЌ
ЁрЁЯOGCЃНІСЃЌ
ЁпЁЯDOBЃН60ЁуЃЌ
ЁрЁЯBCFЃН60ЉІСЃЌ
ЁпЁЯEDBЃН90ЁуЃЌ
ЁрЁЯEBAЃН90ЁуЉІСЃЌ
ЁрЁЯEBAЉЁЯBCFЃН30ЁуЃЌ
ЁрЁЯEBAЉЁЯBCFЕФЖШЪ§ЮЊЖЈжЕЃЎ
ЃЈ3ЃЉШчЭМ1ЫљЪОЃЌвдBЮЊдВаФЃЌBOГЄЮЊАыОЖЛЛЁНЛEDгкЕуMЃЌСЌНгBMЃЌЙ§ЕуCзїEOЕФДЙЯпЃЌНЛEOЕФбгГЄЯпгкЕуNЃЌ
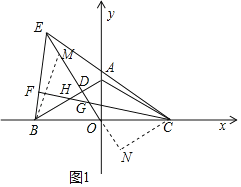
ЁрBMЃНOCЃЌЁЯEMBЃНЁЯGOCЃН120ЁуЃЌ
ЁпЁЯBEMЃНЁЯOGCЃЌ
ЁрЁїEMBЁеЁїGOCЃЈAASЃЉЃЌ
ЁрEMЃНOGЃЌ
ЁрEGЃНMOЃНBOЃН4![]() ЃЌ
ЃЌ
ЁпЁЯCONЃН60ЁуЃЌЁЯNЃН90ЁуЃЌ
ЁрЁЯOCNЃН30ЁуЃЌ
ЁрONЃН![]() OCЃН2
OCЃН2![]() ЃЌ
ЃЌ
ЁрCNЃН6ЃЌ
ЁрSЁїEGCЃНEGCN![]() ЃН4
ЃН4![]() ЁС6ЁС
ЁС6ЁС![]() ЃН12
ЃН12![]() ЃЎ
ЃЎ


 ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
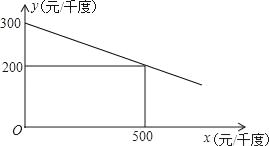
ЁОЬтФПЁПФГЙЄГЇдкЩњВњЙ§ГЬжавЊЯћКФДѓСПЕчФмЃЌЯћКФУПЧЇЖШЕчВњЩњРћШѓгыЕчМлЪЧвЛДЮКЏЪ§ЙиЯЕЃЌОЙ§ВтЫуЃЌЙЄГЇУПЧЇЖШЕчВњЩњРћШѓyЃЈдЊ/ЧЇЖШЃЉЃЉгыЕчМлxЃЈдЊ/ЧЇЖШЃЉЕФКЏЪ§ЭМЯѓШчЭМЃК
ЃЈ1ЃЉЧыЧѓГіyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЮЊСЫЪЕЯжНкФмМѕХХФПБъЃЌгаЙиВПУХЙцЖЈЃЌИУГЇЕчМлxЃЈдЊ/ЧЇЖШЃЉгыУПЬьгУЕчСПmЃЈЧЇЖШЃЉЕФКЏЪ§ЙиЯЕЮЊx=20m+500ЃЌЧвИУЙЄГЇУПЬьгУЕчСПВЛГЌЙ§50ЧЇЖШЃЌЮЊСЫЛёЕУзюДѓРћШѓwЃЌЙЄГЇУПЬьгІАВХХЪЙгУЖрЩйЖШЕчЃПЙЄГЇУПЬьЯћКФЕчВњЩњРћШѓзюДѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛзщЪ§ОнЃКx1ЃЌx2ЃЌx3ЃЌx4ЃЌx5ЃЌx6ЕФЦНОљЪ§ЪЧ2ЃЌЗНВюЪЧ3ЃЌдђСэвЛзщЪ§ОнЃК3x1Љ2ЃЌ3x2Љ2ЃЌ3x3Љ2ЃЌ3x4Љ2ЃЌ3x5Љ2ЃЌ3x6Љ2ЕФЦНОљЪ§КЭЗНВюЗжБ№ЪЧЃЈЁЁЁЁЃЉ
A. 2ЃЌ3 B. 2ЃЌ9 C. 4ЃЌ25 D. 4ЃЌ27
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу AЁЂB дкЪ§жсЩЯБэЪОЕФЪ§ЗжБ№ЮЊЉ12 КЭ 8ЃЌСНжЛТьвЯ MЁЂN ЗжБ№ Дг AЁЂB СНЕуЭЌЪБГіЗЂЃЌЯрЯђЖјааЃЎM ЕФЫйЖШЮЊ 2 ИіЕЅЮЛГЄЖШ/УыЃЌN ЕФЫйЖШЮЊ 3 ИіЕЅЮЛГЄЖШ/УыЃЎ
ЃЈ1ЃЉдЫЖЏ УыжгЪБЃЌСНжЛТьвЯЯргідкЕу PЃЛЕу P дкЪ§жсЩЯБэЪОЕФЪ§ ЪЧ ЃЛ
ЃЈ2ЃЉШєдЫЖЏ t УыжгЪБЃЌСНжЛТьвЯЕФОрРыЮЊ 10ЃЌЧѓГі t ЕФжЕЃЈаДГіНтЬтЙ§ГЬЃЉЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
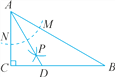
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯCЃН90ЁуЃЌЁЯBЃН30ЁуЃЌвдЕуAЮЊдВаФЃЌШЮвтГЄЮЊАыОЖЛЛЁЃЌЗжБ№НЛABЃЌACгкЕуMКЭNЃЌдйЗжБ№вдЕуMЃЌNЮЊдВаФЃЌДѓгк![]() MNГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌСЌНсAPВЂбгГЄЃЌНЛBCгкЕуDЃЌдђЯТСаЫЕЗЈжаЃЌе§ШЗЕФИіЪ§ЪЧ( )
MNГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌСЌНсAPВЂбгГЄЃЌНЛBCгкЕуDЃЌдђЯТСаЫЕЗЈжаЃЌе§ШЗЕФИіЪ§ЪЧ( )
ЂйADЪЧЁЯBACЕФЦНЗжЯпЃЛЂкЁЯADCЃН60ЁуЃЛЂлЕуDдкABЕФжаДЙЯпЩЯЃЛЂмSЁїDACЁУSЁїABCЃН1ЁУ3.
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЛИіЕуДгЪ§жсЩЯЕФдЕуПЊЪМЃЌЯШЯђгввЦЖЏ2ИіЕЅЮЛГЄЖШЃЌдйЯђзѓвЦЖЏ5ИіЕЅЮЛГЄЖШЃЌПЩвдПДЕНжеЕуБэЪОЪЧ-3ЃЌвбжЊAЁЂBЪЧЪ§жсЩЯЕФЕуЃЌЧыВЮееЯТЭМВЂЫМПМЃЌЭъГЩЯТСаИїЬт.
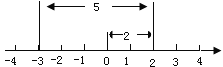
(1)ШчЙћЕуAБэЪОЕФЪ§-1ЃЌНЋЕуAЯђгввЦЖЏ4ИіЕЅЮЛГЄЖШЃЌФЧУДжеЕуBБэЪОЕФЪ§ЪЧ____.AЁЂBСНЕуМфЕФОрРыЪЧ__________.
(2)ШчЙћЕуAБэЪОЕФЪ§2ЃЌНЋЕуAЯђзѓвЦЖЏ6ИіЕЅЮЛГЄЖШЃЌдйЯђгввЦЖЏ3ИіЕЅЮЛГЄЖШЃЌФЧУДжеЕуBБэЪОЕФЪ§ЪЧ____.AЁЂBСНЕуМфЕФОрРыЪЧ____.
(3)ШчЙћЕуAБэЪОЕФЪ§mЃЌНЋЕуAЯђзѓвЦЖЏnИіЕЅЮЛГЄЖШЃЌдйЯђзѓвЦЖЏpИіЕЅЮЛГЄЖШЃЌФЧУДЧыФуВТЯыжеЕуBБэЪОЕФЪ§ЪЧ___.AЁЂBСНЕуМфЕФОрРыЪЧ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌМзввСНЕубизХБпГЄЮЊ3cmЕФе§ЗНаЮЃЌАДAЁњBЁњCЁњDЁњAЁЕФЗНЯђаазпЃЌМзДгAЕувд3cm/sЕФЫйЖШЁЂввДгBЕувдa cm/sЕФЫйЖШЭЌЪБаазпЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌt=2ЪБМзввСНЕуЕквЛДЮЯргі.
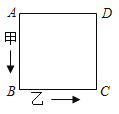
ЃЈ1ЃЉЧѓa
ЃЈ2ЃЉШєaЃО3ЃЌЧвМзввЕквЛДЮЯргіКѓЃЌввЕФЫйЖШБфЮЊ5cm/sЃЌЕБСНЕуЕкЖўДЮЯргіЧАЯрОр4cmЪБЃЌtЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
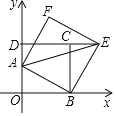
ЁОЬтФПЁПШчЭМЃЌОиаЮOBCDЮЛгкжБНЧзјБъЯЕжаЃЌЕуB(![]() ЃЌ0)ЃЌЕуD(0ЃЌm)дкyжсе§АыжсЩЯЃЌЕуA(0ЃЌ1)ЃЌBEЁЭABЃЌНЛDCЕФбгГЄЯпгкЕуEЃЌвдABЃЌBEЮЊБпзїABEFЃЌСЌНсAEЃЎ
ЃЌ0)ЃЌЕуD(0ЃЌm)дкyжсе§АыжсЩЯЃЌЕуA(0ЃЌ1)ЃЌBEЁЭABЃЌНЛDCЕФбгГЄЯпгкЕуEЃЌвдABЃЌBEЮЊБпзїABEFЃЌСЌНсAEЃЎ
(1)ЕБmЃН![]() ЪБЃЌЧѓжЄЃКЫФБпаЮABEFЪЧе§ЗНаЮЃЎ
ЪБЃЌЧѓжЄЃКЫФБпаЮABEFЪЧе§ЗНаЮЃЎ
(2)МЧЫФБпаЮABEFЕФУцЛ§ЮЊSЃЌЧѓSЙигкmЕФКЏЪ§ЙиЯЕЪНЃЎ
(3)ШєAEЕФжаЕуGЧЁКУТфдкОиаЮOBCDЕФБпЩЯЃЌжБНгаДГіДЫЪБЕуFЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖЏЕуMЁЂNЭЌЪБДгдЕуГіЗЂбиЪ§жсзідШЫйдЫЖЏЃЌМКжЊЖЏЕуMЁЂNЕФдЫЖЏЫйЖШБШЪЧ1ЃК2ЃЈЫйЖШЕЅЮЛЃК1ИіЕЅЮЛГЄЖШ/УыЃЉЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎ
![]()
ЃЈ1ЃЉШєЖЏЕуMЯђЪ§жсИКЗНЯђдЫЖЏЃЌЖЏЕуNЯђЪ§жсе§ЗНЯђдЫЖЏЃЌЕБt=2УыЪБЃЌЖЏЕуMдЫЖЏЕНAЕуЃЌЖЏЕуNдЫЖЏЕНBЕуЃЌЧвAB=12ЃЈЕЅЮЛГЄЖШЃЉЃЎ
ЂйдкЪ§жсЩЯЛГіAЁЂBСНЕуЕФЮЛжУЃЌВЂЛиД№ЃКЕуMдЫЖЏЕФЫйЖШЪЧЁЁ ЁЁЃЈЕЅЮЛГЄЖШ/УыЃЉЃЛЕуNдЫЖЏЕФЫйЖШЪЧЁЁ ЁЁЃЈЕЅЮЛГЄЖШ/УыЃЉЃЎ
ЂкШєЕуPЮЊЪ§жсЩЯвЛЕуЃЌЧвPAЉPB=OPЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжаAЁЂBСНЕуЕФЮЛжУПЊЪМЃЌШєMЁЂNЭЌЪБдйДЮПЊЪМАДдЫйдЫЖЏЃЌЧвдкЪ§жсЩЯЕФдЫЖЏЗНЯђВЛЯоЃЌдйОЙ§МИУыЃЌMN=4ЃЈЕЅЮЛГЄЖШЃЉЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com