
����Ŀ����ͼ������M��Nͬʱ��ԭ������������������˶�����֪����M��N���˶��ٶȱ���1��2���ٶȵ�λ��1����λ����/�룩�����˶�ʱ��Ϊt�룮
![]()
��1��������M�����Ḻ�����˶�������N�������������˶�����t=2��ʱ������M�˶���A�㣬����N�˶���B�㣬��AB=12����λ���ȣ���
���������ϻ���A��B�����λ�ã����ش𣺵�M�˶����ٶ����� ������λ����/�룩����N�˶����ٶ����� ������λ����/�룩��
������PΪ������һ�㣬��PA��PB=OP����![]() ��ֵ��
��ֵ��
��2���ɣ�1����A��B�����λ�ÿ�ʼ����M��Nͬʱ�ٴο�ʼ��ԭ���˶������������ϵ��˶������ޣ��پ������룬MN=4����λ���ȣ���
���𰸡���1����ͼ���������2��4����![]() ��
��![]() ����2��4���8���
����2��4���8���![]() ���
���![]() �룮
�룮
��������
��1���ٸ��������A��B�����ʾ�������ϣ������M��N������ٶȼ��ɣ�
�����P�������϶�Ӧ����Ϊx������PAPB��OP�����x�ķ�Χ�������⼴�ɣ�
��2����������ۣ���M��N�˶��ķ�����ͬ��Ҫʹ��MN=4����ΪN��M����M��N�˶������෴��Ҫʹ��MN=4����ΪM��N������У�Ȼ�����MN��4�ֱ��г�������⼴��.��
�⣺��1���١ߵ�M��N���˶��ٶȱ���1��2��AB=12��
������ᣬ��ͼ��ʾ��
![]()
���M�˶����ٶ���2����λ����/�룩����N�˶����ٶ���4����λ����/�룩��
�����P�������϶�Ӧ����Ϊx��
��PA��PB=OP��0��
��x��2��
��2��x��8ʱ��PA��PB=��x+4������8��x��=x+4��8+x����2x��4=x�����x=4��
��x��8ʱ��PA��PB=��x+4������x��8��=12����x=12��
��![]() ��
��![]() ��
��
��2�����پ���m��MN=4����λ���ȣ���
��M��N�˶��ķ�����ͬ��Ҫʹ��MN=4����ΪN��M��
��|��8��4m��������4��2m��|=4����|12��2m|=4��
��ã�m=4��m=8��
��M��N�˶������෴��Ҫʹ��MN=4����ΪM��N������У�
��|��8��4m��������4+2m��|=4����|12��6m|=4��
��ã�m=![]() ��m=
��m=![]() ��
��
���ϣ��پ���4���8���![]() ���
���![]() �룬MN=4��
�룬MN=4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ����ƽ��ֱ������ϵ�У���A��y���������ϣ���B��C�ֱ���x��ĸ����ᡢ�������ϣ���AB��AC����ACB��30�㣬OD��AB�ڵ�D��
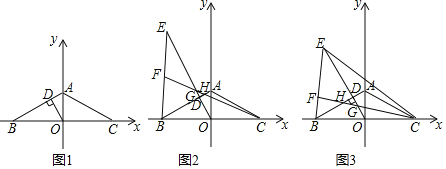
��1����֤��BD��3AD��
��2����ͼ2����E��OD���ӳ����ϣ�����BE�����߶�BE��ȡ��F������CF�ֱ�OE��AB�ڵ�G��H����G��H��D�����غϣ�����FE��FG����֤����EBA����BCF�Ķ���Ϊ��ֵ��
��3����ͼ3���ڣ�2���������£�����EC����C��4![]() ��0����A��0��4������S��ECG��
��0����A��0��4������S��ECG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC ��һ�߳�Ϊ 10�������߳��ֱ��Ƿ��� x2 14 x 48 0 ������������һԲ��ֽƬ������������ȫ���ǣ����Բ��ֽƬ����С�뾶��_______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AE��BC�ڵ�E���ӳ�BC����FʹCF��BE������AF��DE��DF.
(1)��֤���ı���AEFD�Ǿ��Σ�
(2)��AB��6��DE��8��BF��10����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���мƻ������ס���������Ʒ��1200������������Ʒ�Ľ��ۣ��ۼ����±���
���ۣ�Ԫ/���� | �ۼۣ�Ԫ/���� | |
�� | 25 | 30 |
�� | 45 | 60 |
��1��������ν�����������ǡ��Ϊ46000Ԫ��
��2��Ϊȷ������Ʒ�������ڣ�1���������£��̼Ҿ���������Ʒ���д��۳��ۣ���ȫ�����������Ʒ��������Ϊ20%����������Ʒ����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��AOC��60������һֱ�����ǰ�MON��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
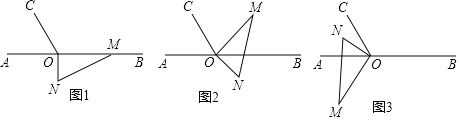
��1�����CON�Ķ�����
��2����ͼ2�ǽ�ͼ1�е����ǰ��Ƶ�O��ÿ��10�����ٶ�����ʱ�뷽����תһ�ܵ����������ת�Ĺ����У�����t��ʱ����������OA��OC��OM������ȵĽǣ����ʱt��ֵ��
��3����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ3��ʹON�ڡ�AOC���ڲ�ʱ����̽����AOM���CON��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и��������������Ӧ�ĺ����ϣ�
�٩�5.32����3���۩�1![]() ����7%����0���ީ�5����0.6����+2019
����7%����0���ީ�5����0.6����+2019
��1��������_____
��2��������_____
��3��������_____
��4��������_____
��5���Ǹ����У�_____
��6����������_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�鳤�Ϳ��ֱ�Ϊ60����40���ij�������Ƥ��Ҫ�������Ľǽ�ȥ�ĸ���ȵ�С�����Σ��۳�һ���ǵij�����ˮ�ۣ�ʹ���ĵ����Ϊ800ƽ������.���ȥ�����εı߳�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����P���߶�AD��һ���㣨�������D�غϣ���PO���ӳ��߽�BC��Q�㣮
��1����֤���ı���PBQDΪƽ���ı��Σ�
��2����AB��6cm��AD��8cm��P�ӵ�A��������1cm/����ٶ����D�����˶������P�˶�ʱ��Ϊt�룬���ı���PBQD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com