
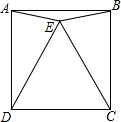
 如图,四边形ABCD是正方形,△CDE是等边三角形,若AE=4cm,则S△AEB=4cm2.
如图,四边形ABCD是正方形,△CDE是等边三角形,若AE=4cm,则S△AEB=4cm2. 分析 作BM⊥AE,交AE延长线于M,由正方形和等边三角形的性质得出AD=DE,∠ADE=30°,由三角形内角和定理得出∠DAE=75°,求出∠ABE=∠BAE,得出BE=AE=4cm,由三角形的外角性质得出∠BEM=30°,求出BM=$\frac{1}{2}$BE=2cm,由三角形的面积公式即可得出结果.
解答 解:作BM⊥AE,交AE延长线于M,如图所示: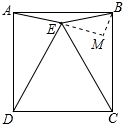
则∠BME=90°,
∵四边形ABCD是正方形,△CDE是等边三角形,
∴∠BAD=∠ABC=∠ADC=∠BCD=90°,AD=CD=BC,DE=CD=CE,∠EDC=∠ECD=60°,
∴AD=DE,∠ADE=30°,
∴∠DAE=$\frac{1}{2}$(180°-30°)=75°,
∴∠BAE=90°-75°=15°,
同理:∠ABE=15°=∠BAE,
∴BE=AE=4cm,∠BEM=∠15°+15°=30°,
∴BM=$\frac{1}{2}$BE=2cm,
∴S△AEB=$\frac{1}{2}$AE×BM=$\frac{1}{2}$×4×2=4(cm2).
故答案为:4.
点评 本题考查了正方形的性质、等边三角形的性质、等腰三角形的性质、三角形内角和定理、含30°角的直角三角形的性质、三角形的外角性质;通过作辅助线求出BM是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
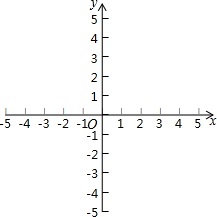 △ABC三个顶点A、B、C的坐标分别为A(2,-1)、B(1,-3)、C(4,-2).
△ABC三个顶点A、B、C的坐标分别为A(2,-1)、B(1,-3)、C(4,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
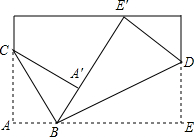 同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.
同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com