
【题目】如图Rt△ABC中,∠ACB=90°,D为AB的中点,E在边AB上,AB=12,BC=6,当ED= ![]() CD,则CE= .
CD,则CE= . 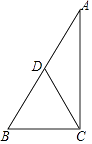
【答案】3 ![]() 或3
或3 ![]()
【解析】解:∵在Rt△ABC中,∠ACB=90°,D为AB的中点,AB=12,BC=6,
∴AD=BD=CD= ![]() AB=6,①如图1,E在AD上,
AB=6,①如图1,E在AD上,
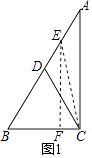
连结CE,过E点作EF⊥BC于F,
∵ED= ![]() CD,
CD,
∴DE=3,
∴BE=9,
∴BF= ![]() BE=4.5,
BE=4.5,
∴在Rt△BFE中,EF= ![]() =
= ![]() ,
,
∵CF=BC﹣BF=6﹣4.5=1.5,
∴在Rt△CFE中,CE= ![]() =3
=3 ![]() ;②如图2,E在BD上,
;②如图2,E在BD上,
连结CE,过E点作EF⊥BC于F,
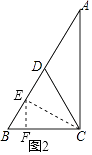
∵ED= ![]() CD,
CD,
∴DE=3,
∴BE=3,
∴BF= ![]() BE=1.5,
BE=1.5,
∴在Rt△BFE中,EF= ![]() =
= ![]() ,
,
∵CF=BC﹣BF=6﹣1.5=4.5,
∴在Rt△CFE中,CE= ![]() =3
=3 ![]() .
.
故CE=3 ![]() 或3
或3 ![]() .
.
所以答案是:3 ![]() 或3
或3 ![]() .
.
【考点精析】本题主要考查了直角三角形斜边上的中线和勾股定理的概念的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.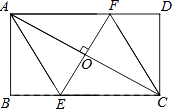
(1)求证:四边形AECF是菱形;
(2)若AB= ![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:①当
的四个命题:①当![]() 时,
时,![]() 有最小值10;②
有最小值10;②![]() 为任何实数,
为任何实数,![]() 时的函数值大于
时的函数值大于![]() 时的函数值;③若
时的函数值;③若![]() ,且
,且![]() 是整数,当
是整数,当![]() 时,
时,![]() 的整数值有
的整数值有![]() 个;④若函数图象过点
个;④若函数图象过点![]() 和
和![]() ,则
,则![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A.① B.② C.③ D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
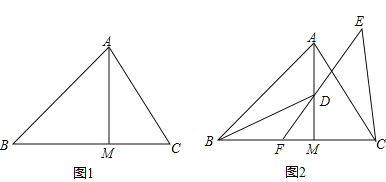
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图1,若AB=3![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com