
【题目】列方程或方程组解应用题:
北京市实施交通管理新措施以来,全市公共交通客运量显著增加.据统计,2008年10月11日到2009年2月28日期间,地面公交日均客运量与轨道交通日均客运量总和为1696万人次,地面公交日均客运量比轨道交通日均客运量的4倍少69万人次.在此期间,地面公交和轨道交通日均客运量各为多少万人次?
科目:初中数学 来源: 题型:
【题目】如图1所示是小明设计的带菱形图案的花边作品,该作品由形如图2所示的矩形图案拼接而成(不重叠,无缝隙),小明发现图(2)具有对称之美,它既是轴对称图形,也是中心对称图形,并对这个图形进行探究.

(1)如图3,若知图案的一部分,请你根据如图2将图3的图案补充完整(要求:尺规作图,保留作图痕迹,不写作法);

(2)如图4,![]() ,
,![]() ,上、下两个阴影部分的面积之和为
,上、下两个阴影部分的面积之和为![]() ,其内部菱形由两组距离相等的平行线两两相交得到,求该菱形的周长;
,其内部菱形由两组距离相等的平行线两两相交得到,求该菱形的周长;
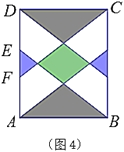
(3)小明认为:图4中的4个空白部分在一定条件下能拼成一个正方形(不重叠,无缝隙),请你帮助小明写出应满足的条件(提示:求出![]() 与
与![]() 的长度之比,并指出点
的长度之比,并指出点![]() 、
、![]() 的位置).
的位置).

查看答案和解析>>
科目:初中数学 来源: 题型:
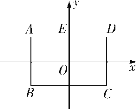
【题目】如图,在平面直角坐标系中,矩形![]() 的对称中心为坐标原点
的对称中心为坐标原点![]() ,
,![]() 轴于点
轴于点![]() (点
(点![]() 在点
在点![]() 的左侧),经过
的左侧),经过![]() 、
、![]() 两点的函数
两点的函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 是常数,图象
是常数,图象![]() 、
、![]() 合起来得到的图象记为
合起来得到的图象记为![]() .设矩形
.设矩形![]() 的周长为
的周长为![]() .
.
(1)当点![]() 的横坐标为-1时,求
的横坐标为-1时,求![]() 的值;
的值;
(2)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当![]() 与矩形
与矩形![]() 恰好有两个公共点时,求
恰好有两个公共点时,求![]() 的值;
的值;
(4)设![]() 在
在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位需购买甲、乙两种消毒剂.经了解,这两种消毒剂的价格都有零售价和批发价(若按批发价,则每种消毒剂购买的数量不少于50桶),零售时甲种消毒剂每桶比乙种消毒剂多8元,已知购买两种消毒剂各![]() (
(![]() )桶,所需费用分别是960元、720元.
)桶,所需费用分别是960元、720元.
(1)求甲、乙两种消毒剂的零售价;
(2)该单位预计批发这两种消毒剂500桶,且甲种消毒剂的数量不少于乙种消毒剂数量的![]() ,甲、乙两种消毒剂的批发价分别为20元/桶、16元/桶.设甲种消毒剂批发数量为
,甲、乙两种消毒剂的批发价分别为20元/桶、16元/桶.设甲种消毒剂批发数量为![]() 桶,购买资金总额为
桶,购买资金总额为![]() (元),请写出
(元),请写出![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最小值和此时的购买方案.
的最小值和此时的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次创建全国文明城市知识竞赛活动,有30名同学参加这次竞赛,成绩分布频数表如下:(单位:分)
成绩(分) | 组中值 | 频数(人数) |
80.5~85.5 | 83 | 3 |
85.5~90.5 | 88 | 6 |
90.5~95.5 | 93 | 12 |
95.5~100.5 | 98 | 9 |
(1)利用组中值计算这30位同学的平均数;
(2)学校根据这次竞赛成绩从高到低选15位同学参加市级比赛,小明同学也参加了这次竞赛,知道自己的成绩后,他想知道自己是否有资格参加市里比赛(学校还未公布到市里比赛名单),他最应关注频数,平均分,众数,中位数中的哪个量?请说明理由;
(3)“创文知识竞赛”中,获一等奖的小红同学得到了印有龚扇、剪纸、彩灯图案的三枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有彩灯图案的概率是多少?请用树状图或列表法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
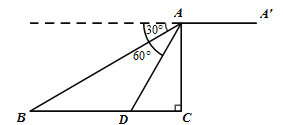
【题目】如图,某无人机于空中![]() 处探测到目标
处探测到目标![]() 的俯角分别是
的俯角分别是![]() ,此时无人机的飞行高度
,此时无人机的飞行高度![]() 为
为![]() ,随后无人机从
,随后无人机从![]() 处继续水平飞行
处继续水平飞行![]() m到达
m到达![]() 处.
处.
(1)求![]() 之间的距离
之间的距离
(2)求从无人机![]() 上看目标
上看目标![]() 的俯角的正切值.
的俯角的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展了防疫知识的宣传教育活动.为了解这次活动的效果,学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分,得分x均为不小于60的整数),并将测试成绩分为四个等第:基本合格(60≤x<70),合格(70≤x<80),良好(80≤x<90),优秀(90≤x≤100),制作了如图统计图(部分信息未给出).
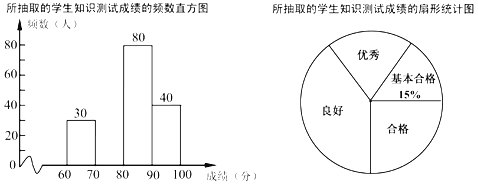
由图中给出的信息解答下列问题:
(1)求测试成绩为合格的学生人数,并补全频数直方图.
(2)求扇形统计图中“良好”所对应的扇形圆心角的度数.
(3)这次测试成绩的中位数是什么等第?
(4)如果全校学生都参加测试,请你根据抽样测试的结果,估计该校获得优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
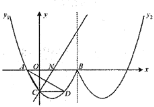
【题目】如图,曲线![]() 是抛物线的一部分,与
是抛物线的一部分,与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且表达式
,且表达式![]() ,曲线
,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求![]() 三点的坐标和曲线
三点的坐标和曲线![]() 的表达式;
的表达式;
(2)过点![]() 作
作![]() 轴交曲线
轴交曲线![]() 于点
于点![]() ,连结
,连结![]() ,在曲线
,在曲线![]() .上有一点
.上有一点![]() ,使得四边形
,使得四边形![]() 为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点
为筝形(如果一个四边形的一条对角线被另一条对角线垂直平分,这样的四边形为筝形),请求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com