
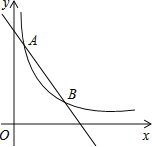
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(1)求反比例函数的表达式
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标
(3)求△PAB的面积.
【答案】(1)反比例函数的表达式y=![]() ,(2)点P坐标(
,(2)点P坐标(![]() ,0), (3)S△PAB= 1.5.
,0), (3)S△PAB= 1.5.
【解析】
(1)把点A(1,a)代入一次函数中可得到A点坐标,再把A点坐标代入反比例解析式中即可得到反比例函数的表达式;(2)作点D关于x轴的对称点D,连接AD交x轴于点P,此时PA+PB的值最小.由B可知D点坐标,再由待定系数法求出直线AD的解析式,即可得到点P的坐标;(3)由S△PAB=S△ABD﹣S△PBD即可求出△PAB的面积.
解:(1)把点A(1,a)代入一次函数y=﹣x+4,
得a=﹣1+4,
解得a=3,
∴A(1,3),
点A(1,3)代入反比例函数y=![]() ,
,
得k=3,
∴反比例函数的表达式y=![]() ,
,
(2)把B(3,b)代入y=![]() 得,b=1
得,b=1
∴点B坐标(3,1);
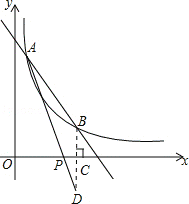
作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,
∴D(3,﹣1),
设直线AD的解析式为y=mx+n,
把A,D两点代入得,![]() ,解得m=﹣2,n=5,
,解得m=﹣2,n=5,
∴直线AD的解析式为y=﹣2x+5,
令y=0,得x=![]() ,
,
∴点P坐标(![]() ,0),
,0),
(3)S△PAB=S△ABD﹣S△PBD=![]() ×2×2﹣
×2×2﹣![]() ×2×
×2×![]() =2﹣
=2﹣![]() =1.5.
=1.5.
点晴:本题是一道一次函数与反比例函数的综合题,并与几何图形结合在一起来求有关于最值方面的问题.此类问题的重点是在于通过待定系数法求出函数图象的解析式,再通过函数解析式反过来求坐标,为接下来求面积做好铺垫.


科目:初中数学 来源: 题型:
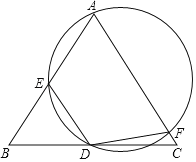
【题目】如图,在△ABC中,AB=AC,点D为BC的中点,经过AD两点的圆分别与AB,AC交于点E、F,连接DE,DF.
(1)求证:DE=DF;
(2)求证:以线段BE+CF,BD,DC为边围成的三角形与△ABC相似,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求抛物线的解析式;
(2)点![]() 在抛物线的对称轴上,当
在抛物线的对称轴上,当![]() 的周长最小时,点
的周长最小时,点![]() 的坐标为_____________;
的坐标为_____________;
(3)点![]() 是第四象限内抛物线上的动点,连接
是第四象限内抛物线上的动点,连接![]() 和
和![]() .求
.求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(4)若点![]() 是对称轴上的动点,在抛物线上是否存在点
是对称轴上的动点,在抛物线上是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 在
在![]() 边上,以
边上,以![]() 为直径的半圆
为直径的半圆![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)已知![]() ,
,![]() 的半径为
的半径为![]() ,求图中阴影部分的面积.(最后结果保留根号和
,求图中阴影部分的面积.(最后结果保留根号和![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
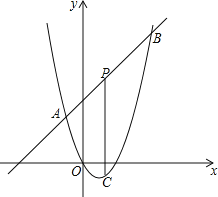
【题目】已知一次函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象相交于
的图象相交于![]() 和
和![]() ,点
,点![]() 是线段
是线段![]() 上的动点(不与
上的动点(不与![]() 重合),过点
重合),过点![]() 作
作![]() 轴,与二次函数
轴,与二次函数![]() 的图象交于点
的图象交于点![]() .
.
(1)求![]() 的值;
的值;
(2)求线段![]() 长的最大值;
长的最大值;
(3)当![]() 为
为![]() 的等腰直角三角形时,求出此时点
的等腰直角三角形时,求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.

(1)该三角形的外接圆的半径长等于 ;
(2)用直尺和圆规作出该三角形的内切圆(不写作法,保留作图痕迹),并求出该三角形内切圆的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com