
【题目】如图,已知E是ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
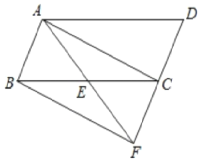
(1)求证:△ABE≌△FCE.
(2)连接AC、BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形。
【答案】(1)见解析;(2)见解析
【解析】
(1)由ABCD为平行四边形,根据平行四边形的对边平行得到AB与DC平行,根据两直线平行内错角相等得到一对角相等,由E为BC的中点,得到两条线段相等,再由对应角相等,利用ASA可得出三角形ABE与三角形FCE全等;
(2)由△ABE与△FCE全等,根据全等三角形的对应边相等得到AB=CF;再由AB与CF平行,根据一组对边平行且相等的四边形为平行四边形得到ABFC为平行四边形,根据平行四边形的对角线互相平分得到AE=EF,BE=EC;再由∠AEC为三角形ABE的外角,利用外角的性质得到∠AEC等于∠ABE+∠EAB,再由∠AEC=2∠ABC,得到∠ABE=∠EAB,利用等角对等边可得出AE=BE,可得出AF=BC,利用对角线相等的平行四边形为矩形可得出ABFC为矩形.
证明:(1)∵四边形ABCD为平行四边形,
∴AB∥DC,
∴∠ABE=∠ECF,
又∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∵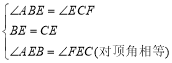 ,
,
∴△ABE≌△FCE(ASA);
(2)∵△ABE≌△FCE,
∴AB=CF,
又∵四边形ABCD为平行四边形,
∴AB∥CF,
∴四边形ABFC为平行四边形,
∴BE=EC,AE=EF,
又∵∠AEC=2∠ABC,且∠AEC为△ABE的外角,
∴∠AEC=∠ABC+∠EAB,
∴∠ABC=∠EAB,
∴AE=BE,
∴AE+EF=BE+EC,即AF=BC,
则四边形ABFC为矩形.


科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小江家的住房户型结构图.根据结构图提供的信息,解答下列问题:
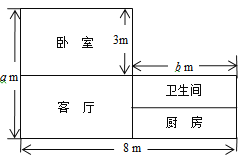
(1)用含a、b的代数式表示小江家的住房总面积S;
(2)小江家准备给房间重新铺设地砖.若卧室所用的地砖价格为每平方米50元;卫生间、厨房和客厅所用的地砖价格为每平方米40元.请用含a、b的代数式表示铺设地砖的总费用W;
(3)在(2)的条件下,当a=6,b=4时,求W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
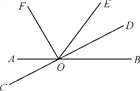
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,货轮A在航行过程中,发现灯塔B在它北偏东60°的方向上,货轮C在它南偏东30°方向上.则下列结论:①∠NAB=60°;②∠WAC=120°;③图中∠NAC的补角有两个,分别是∠SAC和∠EAB;④图中有4对互余的角,其中正确的个数有( )
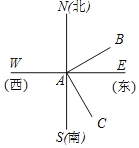
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A和点B在数轴上对应的数分别为a和b,且(a+6)2+|b﹣8|=0.
(1)求线段AB的长;
(2)点C在数轴上所对应的数为x,且x是方程x﹣1=![]() x+1的解,在线段AB上是否存在点D,使得AD+BD=
x+1的解,在线段AB上是否存在点D,使得AD+BD=![]() CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
(3)在(2)的条件下,线段AD和BC分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为t秒,M为线段AD的中点,N为线段BC的中点,若MN=12,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
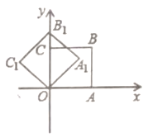
【题目】如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到正方形
后得到正方形![]() ,依此方式,绕点
,依此方式,绕点![]() 连续旋转2019次得到正方形
连续旋转2019次得到正方形![]() ,如果点
,如果点![]() 的坐标为(1,0),那么点
的坐标为(1,0),那么点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.

(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 平均数是 中位数为
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
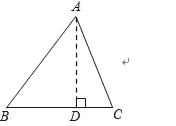
【题目】在△ABC中,AB=30,BC=28,AC=26.求△ABC的面积.
某学习小组经过合作交流给出了下面的解题思路,请你按照他们的解题思路完成解答过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com