Question

7．如图，A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O得切线，与CA的延长线相交于点E，G是AD的中点，连接CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．
（1）求证：BF=EF；
（2）求证：PA是⊙O的切线．

Answer 1

分析 （1）根据切线判定知道EB⊥BC，而AD⊥BC，从而可以确定AD∥BE，那么△BFC∽△DGC，又G是AD的中点，就可得出结论BF=EF．
（2）要证PA是⊙O的切线，就要证明∠PAO=90°，连接AO，AB，根据（1）的结论和BE是⊙O的切线和直角三角形的等量代换，就可得出结论．

解答 解：（1）∵BC是⊙O的直径，BE是⊙O的切线，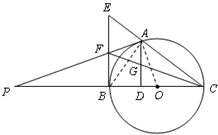
∴EB⊥BC．
又∵AD⊥BC，
∴AD∥BE，
∴△BFC∽△DGC，△FEC∽△GAC，
∴$\frac{BF}{DG}$=$\frac{CF}{CG}$，$\frac{EF}{AG}$=$\frac{CF}{CG}$，
∴$\frac{BF}{DG}$=$\frac{EF}{AG}$，
∵G是AD的中点，
∴DG=AG，
∴BF=EF．
（2）连结AO，AB，
∵BC是⊙O的直径，
∴∠BAC=90°．
在Rt△BAE中，由（1）知F是斜边BE的中点，
∴AF=FB=EF，
∴∠FBA=∠FAB  
 又∵OA=OB，
∴∠ABO=∠BAO
∵BE是⊙O的切线，
∴∠EBO=90°
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°
∴PA是⊙O的切线．

点评 本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．