
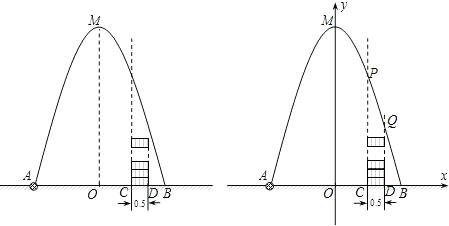
分析 (1)根据题意顶点M(0,4)、点A(-2,0),利用待定系数法可求出函数解析式;
(2)当桶的左侧(x=1)最高点位于抛物线以下,右侧(x=1.5)最高点位于抛物线以上时,球才能落入桶内,
据此可分别计算x=1和x=1.5时y的值,与桶高4×0.4比较可知;
(3)可设桶的个数为m,根据(2)中关系列出不等式,即可求出m的范围.
解答 解:(1)∵网球飞行的最大高度OM=4m,
∴OM所在直线是抛物线的对称轴,
∵AB=4m,
∴AO=BO=2m,
∴A(-2,0),顶点M(0,4),
故可设网球飞行路线的抛物线解析式为:y=ax2+4,
把A(-2,0)代入得:4a+4=0,解得:a=-1,
∴网球飞行路线的抛物线解析式为:y=-x2+4;
(2)∵CD=0.5,AC=3且AO=2,
∴OC=1,OD=1.5,即点Q的横坐标是1.5,点P的横坐标是1,
∴当x=1时,y=3;当x=1.5时,y=1.75;
若竖直摆放4个圆柱形桶,则桶高为4×0.4=1.6m,
而4×0.4<1.75,且4×0.4<3,
∴若竖直摆放4个圆柱形桶时,网球不能落入桶内;
(3)设竖直摆放的圆柱形桶有m个时,网球能落入桶内,
则1.75<0.4m<3,
解得:4.375<m<7.5,
∵m为整数,
∴m的值为5或6或7,
答:当竖直摆放5个或6个或7个圆形桶时,网球能落入桶内.
点评 本题主要考查待定系数法求二次函数解析式及二次函数的实际应用,求能否落入桶内时高度的比较关系是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 7a2+3a+8-(5a2-3a+8)=2a2 | B. | 3a+5b-3c-3a+7b-6c=12b-9 | ||
| C. | 3x-2y-[4x-3(x-y)]=2x-5y | D. | 5(a+b)+4(a+b)-12(a-b)=-3a-3b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O得切线,与CA的延长线相交于点E,G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O得切线,与CA的延长线相交于点E,G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100元 | B. | 150元 | C. | 200元 | D. | 250元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
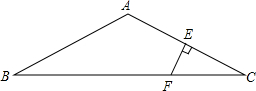 如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.
如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com