
【题目】如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
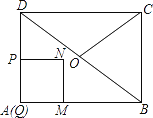
(1)求点N落在BD上时t的值;
(2)直接写出点O在正方形PQMN内部时t的取值范围;
(3)当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;
(4)直接写出直线DN平分△BCD面积时t的值.
【答案】(1)![]() ;(2)2<t<
;(2)2<t< ![]() ;(3)见解析; (4)t的值为
;(3)见解析; (4)t的值为 ![]() 、
、 ![]() 、
、 ![]() .
.
【解析】
试题(1)根据条件证明△DPN∽△DQB然后利用对应边成比例得出关于t的方程,解方程即可;(2)只需考虑求出两个临界位置①MN经过点O,②点P与点O重合下t的值即可;(3)①分0<t![]() ,
,![]() <t≤6,6<t≤11三种情况讨论,根据图形面积公式或和差关系即可用t表示出面积s;②因为点P在折线AD-DO运动,所以可分点P在AD上,点P在DO上,两种情况讨论.
<t≤6,6<t≤11三种情况讨论,根据图形面积公式或和差关系即可用t表示出面积s;②因为点P在折线AD-DO运动,所以可分点P在AD上,点P在DO上,两种情况讨论.
试题解析:(1)当点N落在BD上时,
∵四边形PQMN是正方形,∴PN∥QM,PN=PQ=t.
∴△DPN∽△DQB.∴![]() .
.
∵PN=PQ=PA=t,DP=6﹣t,QB=AB=8,∴![]() .∴t=
.∴t=![]()
∴当t=![]() 时,点N落在BD上. (2分)
时,点N落在BD上. (2分)
(2)当点O在正方形PQMN内部时,t的范围是4<t<11(5分)
(3)①当0<t![]() 时,如图4.
时,如图4.
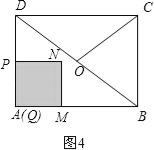
S=S正方形PQMN=PQ2=PA2=t2.
当![]() <t≤6时,如图5,
<t≤6时,如图5,
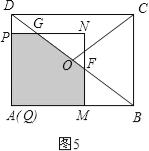
∵tan∠ADB=![]() =
=![]() ,∴
,∴![]() =
=![]() .∴PG=8﹣
.∴PG=8﹣![]() t.
t.
∴GN=PN﹣PG=t﹣(8﹣![]() t)=
t)=![]() ﹣8.
﹣8.
∵tan∠NFG=tan∠ADB=![]() ,∴
,∴![]() .
.
∴NF=![]() GN=
GN=![]() (
(![]() ﹣8)=
﹣8)=![]() t﹣6.
t﹣6.
∴S=S正方形PQMN﹣S△GNF=t2﹣![]() ×(
×(![]() ﹣8)×(
﹣8)×(![]() t﹣6)
t﹣6)
=﹣![]() t2+14t﹣24.
t2+14t﹣24.
当6<t≤11时,如图6,
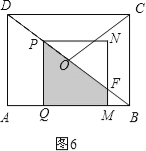
∵四边形PQMN是正方形,四边形ABCD是矩形.
∴∠PQM=∠DAB=90°.∴PQ∥AD.∴△BQP∽△BAD.
∴![]() =
=![]() =
=![]() .∵BP=16﹣t,BD=10,BA=8,AD=6,
.∵BP=16﹣t,BD=10,BA=8,AD=6,
∴![]() .∴BQ=
.∴BQ=![]() ,PQ=
,PQ=![]() .
.
∴QM=PQ=![]() .∴BM=BQ﹣QM=
.∴BM=BQ﹣QM=![]() .
.
∵tan∠ABD=![]() ,∴FM=
,∴FM=![]() BM=
BM=![]() .
.
∴S=S梯形PQMF=![]() (PQ+FM)QM=
(PQ+FM)QM=![]() [
[![]() +
+![]() ]
]![]()
=![]() (16﹣t)2=
(16﹣t)2=![]() t2-
t2-![]()
综上所述:当0<t≤![]() 时,S=t2.
时,S=t2.
当![]() <t≤6时,S=﹣
<t≤6时,S=﹣![]() t2+14t﹣24.
t2+14t﹣24.
当6<t≤11时,S=![]() t2-
t2-![]()
②当直线DN平分△BCD面积时,t的值为![]() 、
、![]()


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
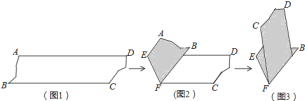
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目:初中数学 来源: 题型:
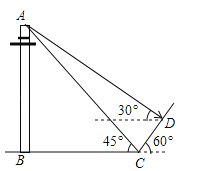
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
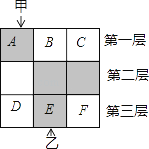
(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
②黑色方块所构拼图是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
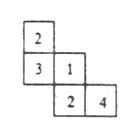
【题目】一个几何体由大小相同的棱长为1的小立方块搭成,从上面看到几何体的形状如图所示,其中小正方形中的数字表示该位置的小立方块的个数.
(1)请画出从正面和从左面看到这个几何体的形状.
(2)求这个几何体的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
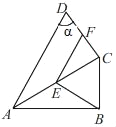
【题目】如图,四边形ABCD中,AC平分∠BAD,∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=α,则∠BEF的度数为_____(用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com