
【题目】如图,四边形ABCD中,AC平分∠BAD,∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=α,则∠BEF的度数为_____(用含α的式子表示).
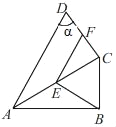
【答案】270°﹣3α
【解析】根据直角三角形的性质得到∠DAC=90°﹣α,根据角平分线的定义、三角形的外角的性质得到∠CEB=180°﹣2α,根据三角形中位线定理、平行线的性质得到∠CEF=∠D=α,结合图形计算即可.
∵∠ACD=90°,∠D=α,
∴∠DAC=90°﹣α,
∵AC平分∠BAD,
∴∠DAC=∠BAC=90°﹣α,
∵∠ABC=90°,EAC的中点,
∴BE=AE=EC,
∴∠EAB=∠EBA=90°﹣α,
∴∠CEB=180°﹣2α,
∵E、F分别为AC、CD的中点,
∴EF∥AD,
∴∠CEF=∠D=α,
∴∠BEF=180°﹣2α+90°﹣α=270°﹣3α,
故答案为:270°﹣3α.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知P(-3,m)和Q(1,m)是抛物线y=2x2+bx+1上的两点.
(1)求b的值;
(2)若A(-2,y1),B(5,y2)是抛物线y=2x2+bx+1上的两点,试比较y1与y2的大小关系;
(3)将抛物线y=2x2+bx+1的图象向上平移k(k是正整数)个单位长度,使平移后的图象与x轴无交点,求k的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区要调查社区居民双休日的学习状况,采用下列调查方式:

①从一幢高层住宅楼中选取200名居民;
②从不同住宅楼中随机选取200名居民;
③选取社区内200名在校学生.
(1)上述调查方式最合理的是 ;
(2)将最合理的调查方式得到的数据制成扇形统计图(如图1)和频数分布直方图(如图2),在这个调查中,200名居民双休日在家学习的有 人;
(3)请估计该社区2 000名居民双休日学习时间不少于4小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
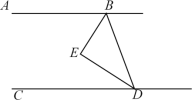
【题目】如图,AB∥CD,BE平分∠ABD,DE平分∠BDC。
(1)求证:BE⊥DE;
(2)H是直线CD上一动点(不与D重合),HI平分∠HBD交CD于点I。请你画出图形,并猜想∠EBI与∠BHD的数量关系,且说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生参加“经典诵读”的活动情况.该校随机选取部分学生,对他们在三、四月份的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
四月份日人均诵读时间的统计表
日人均诵读时间 | 人数 | 百分比 |
| 6 | |
| 30 | |
|
|
|
| 10 |
|
|
|
|
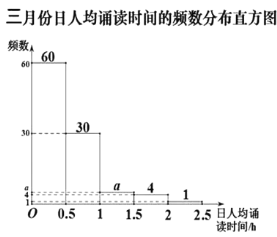
根据以上信息,解答下列问题:
(1)本次调查的学生人数为______;
(2)图表中的![]() ,
,![]() ,
,![]() ,
,![]() 的值分别为______,______,______,______;
的值分别为______,______,______,______;
(3)在被调查的学生中,四月份日人均诵读时间在![]() 范围内的人数比三月份在此范围的人数多______人.
范围内的人数比三月份在此范围的人数多______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在四边形ABCD中,A、B、C、D四个点的坐标分别是:(-2,0)、(0,6)、(4,4)、(2,0)现将四边形ABCD先向上平移1个单位,再向左平移2个单位,平移后的四边形是A'B'C′D'
(1)请画出平移后的四边形A'B'C′D'(不写画法),并写出A'、B'、C′、D'四点的坐标.
(2)若四边形内部有一点P的坐标为(a,b)写点P的对应点P′的坐标.
(3)求四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com