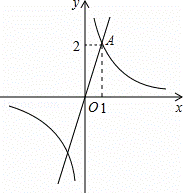
如图，已知点A（1，2）是正比例函数y1=kx（k≠0）与反比例函数y2=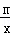
（m≠0）的一个交点．
（1）求正比例函数及反比例函数的表达式；
（2）根据图象直接回答：在第一象限内，当x取何值时，y1＜y2？
阅读快车系列答案科目：初中数学 来源： 题型：
如图为一次函数y=kx+b（k≠0）的图象，则下列正确的是（ ）
A． k＞0，b＞0 B． k＞0，b＜0 C． k＜0，b＞0 D． k＜0，b＜0
查看答案和解析>>
科目：初中数学 来源： 题型：
阅读下面的材料：
如果函数y=f（x）满足：对于自变量x的取值范围内的任意x1，x2，
（1）若x1＜x2，都有f（x1）＜f（x2），则称f（x）是增函数；
（2）若x1＜x2，都有f（x1）＞f（x2），则称f（x）是增函数．
例题：证明函数f（x）=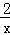
（x＞0）是减函数．
证明：假设x1＜x2，且x1＞0，x2＞0
f（x1）﹣f（x2）=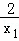
﹣
=
=
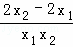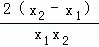
∵x1＜x2，且x1＞0，x2＞0
∴x2﹣x1＞0，x1x2＞0
∴
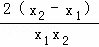＞0，即f（x1）﹣f（x2）＞0
∴f（x1）＞f（x2）
∴函数f（x）=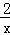
（x＞0）是减函数．
根据以上材料，解答下面的问题：
（1）函数f（x）=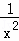
（x＞0），f（1）=
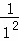=1，f（2）=
=
．
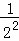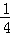计算：f（3）=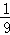 
，f（4）= 
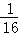，猜想f（x）=
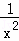（x＞0）是 减 函数（填“增”或“减”）；
查看答案和解析>>
科目：初中数学 来源： 题型：
某公司欲招聘一名工作人员，对甲、乙两位应聘者进行面试和笔试，他们的成绩（百分制）如下表所示．
| 应聘者 | 面试 | 笔试 |
| 甲 | 87 | 90 |
| 乙 | 91 | 82 |
若公司分别赋予面试成绩和笔试成绩6和4的权，计算甲、乙两人各自的平均成绩，谁将被录取？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
0），反比例函数y2=
；
D． ﹣