
阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是增函数.
例题:证明函数f(x)=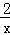 (x>0)是减函数.
(x>0)是减函数.
证明:假设x1<x2,且x1>0,x2>0
f(x1)﹣f(x2)=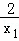 ﹣
﹣ =
=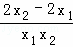 =
=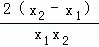
∵x1<x2,且x1>0,x2>0
∴x2﹣x1>0,x1x2>0
∴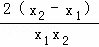 >0,即f(x1)﹣f(x2)>0
>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)=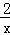 (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
(1)函数f(x)=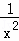 (x>0),f(1)=
(x>0),f(1)=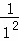 =1,f(2)=
=1,f(2)=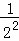 =
=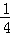 .
.
计算:f(3)= 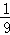 ,f(4)=
,f(4)= 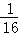 ,猜想f(x)=
,猜想f(x)=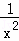 (x>0)是 减 函数(填“增”或“减”);
(x>0)是 减 函数(填“增”或“减”);
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
在一个不透明的口袋装有三个完全相同的小球,分别标号为1、2、3.求下列事件的概率:
(1)从中任取一球,小球上的数字为偶数;
(2)从中任取一球,记下数字作为点A的横坐标x,把小球放回袋中,再从中任取一球记下数字作为点A的纵坐标y,点A(x,y)在函数y=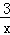 的图象上.
的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
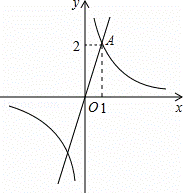
如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=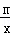 (m≠0)的一个交点.
(m≠0)的一个交点.
(1)求正比例函数及反比例函数的表达式;
(2)根据图象直接回答:在第一象限内,当x取何值时,y1<y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图4,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是
A.线段AE的中垂线与线段AC的中垂线的交点
B .线段AB的中垂线与线段AC的中垂线的交点
.线段AB的中垂线与线段AC的中垂线的交点
C.线段AE的中垂线与线段BC的中垂线的交点
D.线段AB的中垂线与线段BC的中垂线的交点
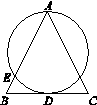 图4
图4
查看答案和解析>>
科目:初中数学 来源: 题型:
已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB ,
延长DA,CB相交于点E.
(1)如图11,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图12,连接OE,过点E作直线EF,使得∠OEF=30°.
当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.
 | |||
 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
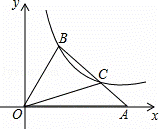
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=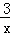 (x>0)的图象上,则△OAB的面积等于 .
(x>0)的图象上,则△OAB的面积等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com