
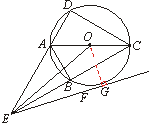
已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB ,
延长DA,CB相交于点E.
(1)如图11,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图12,连接OE,过点E作直线EF,使得∠OEF=30°.
当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.
 | |||
 | |||
(1)证明:∵四边形ABCD内接于⊙O,∠ADC=90°,
∴∠ABC=90°.
 ∴∠ABE=90°.
∴∠ABE=90°.
∵AC平分∠DCB,
∴∠ACB=∠ACD.
∴AB=AD.
∵EB=AD,
∴EB=AB.
∴△ABE是等腰直角三角形.
(2)直线EF与⊙O相离.
证明:过O作OG⊥EF,垂足为G.
 在Rt△OEG中,
在Rt△OEG中,
∵∠OEG=30°,
∴OE=2OG.
∵∠ADC=90°,
∴AC是直径.
设∠ACE=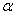 ,AC=2r.
,AC=2r.
由(1)得∠DCE=2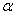 ,
,
又∠ADC=90°,
∴∠AEC=90°-2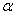 .
.
∵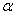 ≥30°,
≥30°,
∴(90°-2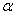 )-
)-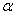 ≤0.
≤0.
∴∠AEC≤∠ACE.
∴AC≤AE.
在△AEO中,∠EAO=90°+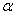 ,
,
∴∠EAO>∠AOE.
∴EO>AE.
∴EO-AE>0.
由AC≤AE得AE-AC≥0.
∴EO-AC=EO+AE-AE-AC
=(EO-AE)+(AE-AC)>0.
∴EO>AC.
即2OG≥2r.
∴OG>r.
∴直线EF与⊙O相离.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
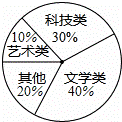
A. 800 B. 600 C. 400 D. 200
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是增函数.
例题:证明函数f(x)=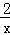 (x>0)是减函数.
(x>0)是减函数.
证明:假设x1<x2,且x1>0,x2>0
f(x1)﹣f(x2)=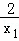 ﹣
﹣ =
=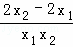 =
=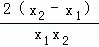
∵x1<x2,且x1>0,x2>0
∴x2﹣x1>0,x1x2>0
∴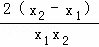 >0,即f(x1)﹣f(x2)>0
>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)=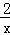 (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
(1)函数f(x)=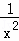 (x>0),f(1)=
(x>0),f(1)=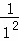 =1,f(2)=
=1,f(2)=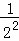 =
=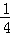 .
.
计算:f(3)= 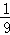 ,f(4)=
,f(4)= 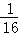 ,猜想f(x)=
,猜想f(x)=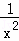 (x>0)是 减 函数(填“增”或“减”);
(x>0)是 减 函数(填“增”或“减”);
查看答案和解析>>
科目:初中数学 来源: 题型:
某公司欲招聘一名工作人员,对甲、乙两位应聘者进行面试和笔试,他们的成绩(百分制)如下表所示.
| 应聘者 | 面试 | 笔试 |
| 甲 | 87 | 90 |
| 乙 | 91 | 82 |
若公司分别赋予面试成绩和笔试成绩6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
某中学为开拓学生视野,开展“课外读 书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
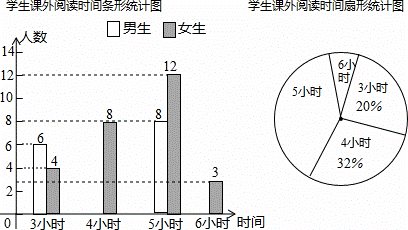
(1)本次调查的学生总数为 人,被调查学生的课外阅读时间的中位数是 小时,众数是 小时;
(2)请你补全条形统计图;
(3)在扇形统计图中,课 外阅读时间为5小时的扇形的圆心角度数是 ;
外阅读时间为5小时的扇形的圆心角度数是 ;
(4)若全校九年级共有学生700人,估计九年级一周课外阅读时间为6小时的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com