
【题目】如图,抛物线![]() 过点A(
过点A(![]() ,2),且与直线
,2),且与直线![]() 交于B、C两点,点B的坐标为(
交于B、C两点,点B的坐标为(![]() ,m).
,m).
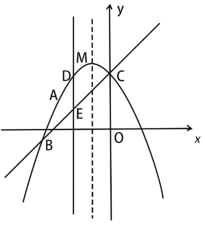
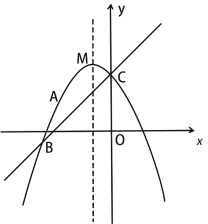
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线BC上方的一点,过点D作DE⊥x轴交直线BC于点E,点P为对称轴上一动点,当线段DE的长度最大时,求PD+PA的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使得∠AQM=45°?若存在,求点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)PD+PA的最小值为
;(2)PD+PA的最小值为![]() ;(3)Q1(0,2-
;(3)Q1(0,2-![]() )、Q2(0,2+
)、Q2(0,2+![]() ).
).
【解析】
(1)将点B的坐标为(-4,m)代入![]() ,
,![]() ,B的坐标为(-4,
,B的坐标为(-4,![]() ),将A(-3,2),B(-4,
),将A(-3,2),B(-4,![]() )代入y=
)代入y=![]() x2+bx+c,解得b=-1,c=
x2+bx+c,解得b=-1,c=![]() ,因此抛物线的解析式y=
,因此抛物线的解析式y=![]() x2-x+
x2-x+![]() ;
;
(2)设D(m,![]() m2-m+
m2-m+![]() ),则E(m,m+
),则E(m,m+![]() ),DE=(
),DE=(![]() m2-m+
m2-m+![]() )-(m+
)-(m+![]() )=
)=![]() m2-2m=
m2-2m=![]() (m+2)2+2,当m=-2时,DE有最大值为2,此时D(-2,
(m+2)2+2,当m=-2时,DE有最大值为2,此时D(-2,![]() ),作点A关于对称轴的对称点A',连接A'D,与对称轴交于点P.PD+PA=PD+PA'=A'D,此时PD+PA最小;
),作点A关于对称轴的对称点A',连接A'D,与对称轴交于点P.PD+PA=PD+PA'=A'D,此时PD+PA最小;
(3)作AH⊥对称轴于点H,连接![]() ∠AHM,可知△AQM外接圆的圆心为H,于是QH=HA=HM=2设Q(0,t),则
∠AHM,可知△AQM外接圆的圆心为H,于是QH=HA=HM=2设Q(0,t),则![]() ,t=2+
,t=2+![]() 或2-
或2-![]() ,求得符合题意的点Q的坐标:Q1(0,2-
,求得符合题意的点Q的坐标:Q1(0,2-![]() )、Q2(0,2+
)、Q2(0,2+![]() ).
).
解:(1)将点B的坐标为(-4,m)代入![]() ,得m=-4+
,得m=-4+![]() =-
=-![]() ,
,
∴B的坐标为(-4,-![]() ),
),
将A(-3,2),B(-4,-![]() )代入y=-
)代入y=-![]() x2+bx+c,
x2+bx+c,
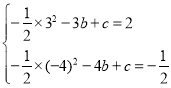
解得b=-1,c=![]() ,
,
∴抛物线的解析式y=![]() x2-x+
x2-x+![]() ;
;
(2)设D(m,![]() m2-m+
m2-m+![]() ),则E(m,m+
),则E(m,m+![]() ),
),
DE=(![]() m2-m+
m2-m+![]() )-(m+
)-(m+![]() )=
)=![]() m2-2m=-
m2-2m=-![]() (m+2)2+2,
(m+2)2+2,
∴当m=-2时,DE有最大值为2,
此时D(-2,![]() ),
),
作点A关于对称轴的对称点A',连接A'D,与对称轴交于点P.
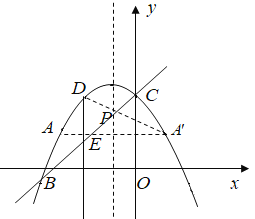
PD+PA=PD+PA'=A'D,此时PD+PA最小,
∵A(-3,2),
∴A'(1,2),
A'D=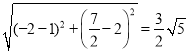 ,
,
即PD+PA的最小值为![]() ;
;
(3)作AH⊥对称轴于点H,连接AM、AQ、MQ、HA、HQ,
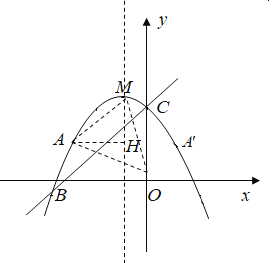
∵抛物线的解析式![]() ,
,
∴M(-1,4),
∵A(-3,2),
∴AH=MH=2,H(-1,2)
∵∠AQM=45°,∠AHM=90°,
∴∠AQM=![]() ∠AHM,
∠AHM,
可知△AQM外接圆的圆心为H,
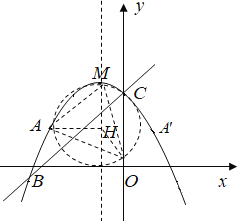
∴QH=HA=HM=2
设Q(0,t),
则![]() ,
,
解得,t=2+![]() 或2-
或2-![]()
∴符合题意的点Q的坐标:Q1(0,2-![]() )、Q2(0,2+
)、Q2(0,2+![]() ).
).


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=8,BC=6,点D是射线CB上一动点,以每秒2个单位长度的速度从C出发向B运动,以CA,CD为边作矩形ACDE,直线AB与直线CE、DE的交点分别为F,G.设点D运动的时间为t(s).
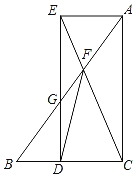
(1)BD= (用含t的代数式表示).
(2)当四边形ACDE是正方形时,求GF的长.
(3)当t为何值时,△DFG为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
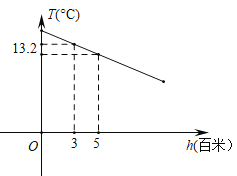
【题目】某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
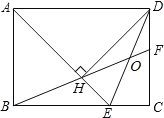
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BCCF=2HE.其中正确的结论有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BCCF=2HE.其中正确的结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
组别 | 分数段 | 频数(人) | 频率 |
1 | 50≤x<60 | 30 | 0.1 |
2 | 60≤x<70 | 45 | 0.15 |
3 | 70≤x<80 | 60 | n |
4 | 80≤x<90 | m | 0.4 |
5 | 90≤x<100 | 45 | 0.15 |
请根据以图表信息,解答下列问题:
(1)表中m= ,n= ;
(2)补全频数分布直方图;
(3)全体参赛选手成绩的中位数落在第几组;
(4)若得分在80分以上(含80分)的选手可获奖,记者从所有参赛选手中随机采访1人,求这名选手恰好是获奖者的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
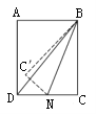
【题目】如图,在矩形ABCD中,AB=3,BC=4,点N为边DC上一动点(不与C、D重合),连接BN,作C关于直线BN的对称点C′连接B C′, C′N,当C′恰好在△ABD的边上时,CN的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,C为⊙O上一点,OC=4,∠OAC=60°.
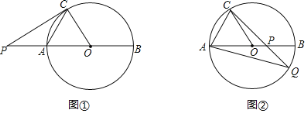
(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小及PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年初,新冠肺炎肆虐全球.我国政府和人民采取了积极有效的防疫措施,疫情在我国得到了有效控制.小明为复学到药店购买![]() 口罩和一次性医用口罩.已知购买
口罩和一次性医用口罩.已知购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用口罩共需
个一次性医用口罩共需![]() 元;购买
元;购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用罩共需
个一次性医用罩共需![]() 元.
元.
(1)求![]() 口罩与一次性医用口罩的单价;
口罩与一次性医用口罩的单价;
(2)小明准备购买![]() 口罩和一次性医用口罩共
口罩和一次性医用口罩共![]() 个,且
个,且![]() 口罩的数量不少于一次性医用口罩数量的
口罩的数量不少于一次性医用口罩数量的![]() .请设计出最省钱的购买方案,并说明理由.
.请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com