
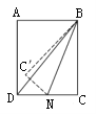
【题目】如图,在矩形ABCD中,AB=3,BC=4,点N为边DC上一动点(不与C、D重合),连接BN,作C关于直线BN的对称点C′连接B C′, C′N,当C′恰好在△ABD的边上时,CN的长为__________.
科目:初中数学 来源: 题型:
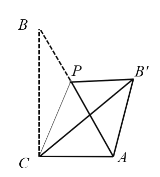
【题目】已知,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,点P是AB上一点,连接CP,将∠B沿CP折叠,使点B落在B'处.以下结论正确的有________
①当AB'⊥AC时,AB'的长为![]() ;
;
②当点P位于AB中点时,四边形ACPB'为菱形;
③当∠B'PA=30°时,![]() ;
;
④当CP⊥AB时,AP:AB':BP=1:2:3.
查看答案和解析>>
科目:初中数学 来源: 题型:
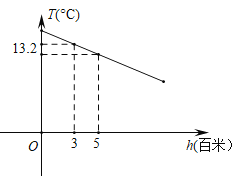
【题目】某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
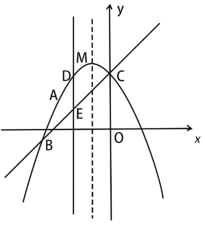
【题目】如图,抛物线![]() 过点A(
过点A(![]() ,2),且与直线
,2),且与直线![]() 交于B、C两点,点B的坐标为(
交于B、C两点,点B的坐标为(![]() ,m).
,m).
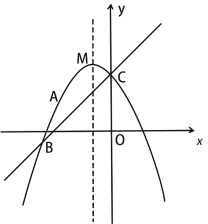
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线BC上方的一点,过点D作DE⊥x轴交直线BC于点E,点P为对称轴上一动点,当线段DE的长度最大时,求PD+PA的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使得∠AQM=45°?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一项工程,由甲、乙两个工程队共同完成,若乙工程队单独完成需要60天;若两个工程队合作18天后,甲工程队再单独做10天也恰好完成.
(1)甲工程队单独完成此项工程需要几天?
(2)若甲工程队每天施工费用为0.6万元,乙工程队每天施工费用为0.35万元,要使该项目总施工费用不超过22万元,则乙工程队至少施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,点D为直线BC上的一动点
,点D为直线BC上的一动点![]() 点D不与点B、C重合
点D不与点B、C重合![]() ,以AD为边作
,以AD为边作![]() ,使
,使![]() ,
,![]() ,连接CE.
,连接CE.
发现问题:
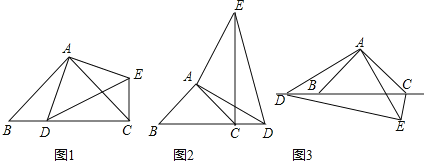
如图1,当点D在边BC上时,
![]() 请写出BD和CE之间的位置关系为______,并猜想BC和CE、CD之间的数量关系:______.
请写出BD和CE之间的位置关系为______,并猜想BC和CE、CD之间的数量关系:______.
尝试探究:
![]() 如图2,当点D在边BC的延长线上且其他条件不变时,
如图2,当点D在边BC的延长线上且其他条件不变时,![]() 中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
拓展延伸:
![]() 如图3,当点D在边CB的延长线上且其他条件不变时,若
如图3,当点D在边CB的延长线上且其他条件不变时,若![]() ,
,![]() ,求线段ED的长.
,求线段ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
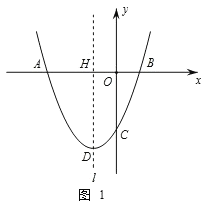
【题目】如图1,已知抛物线![]() 经过A(-3,0),B(1,0),C(0,-3)三点,其顶点为D,对称轴是直线
经过A(-3,0),B(1,0),C(0,-3)三点,其顶点为D,对称轴是直线![]() ,
,![]() 与x轴交于点H.
与x轴交于点H.
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴![]() 上的一个动点,求△PBC周长的最小值;
上的一个动点,求△PBC周长的最小值;
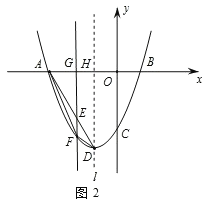
(3)如图2,若E是线段AD上的一个动点(E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①试求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个运输小队分别从两个仓库以相同的工作效率调运一批物资,两队同时开始工作.第二小队工作5天后,由于技术问题检修设备5天,为赶上进度,再次开工后他们将工作效率提高到原先的2倍,结果和第一小队同时完成任务.在两队调运物资的过程中,两个仓库物资的剩余量y t与第一小队工作时间x天的函数图像如图所示.

(1)①求线段AC所表示的y与x之间的函数表达式;
②求点F的坐标,并解释点F的实际意义.
(2)如果第二小队没有检修设备,按原来的工作效率正常工作,那么他们完成任务的天数是 天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.
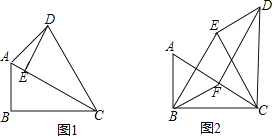
(1)当点E恰好在AC上时,如图1,求∠ADE的大小;
(2)若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com