
【题目】如图①,元旦期间,小明乘汽车从![]() 地出发,经过
地出发,经过![]() 地到目的地
地到目的地![]() 地(三地在同一条直线上),假设汽车从
地(三地在同一条直线上),假设汽车从![]() 到
到![]() 的过程都是匀速直线行驶.图②表示小明离
的过程都是匀速直线行驶.图②表示小明离![]() 地的路程
地的路程![]() (km)与汽车从
(km)与汽车从![]() 出发后行驶时间
出发后行驶时间![]() (h)之何的函数关系图像.
(h)之何的函数关系图像.
(1)![]() 两地间的路程为 km;
两地间的路程为 km;
(2)求小明离![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(3)当行驶时间![]() 在什么范围时,汽车离
在什么范围时,汽车离![]() 地的路程不超过40 km?
地的路程不超过40 km?

【答案】(1)160;(2)当![]() 时,表达式为:
时,表达式为:![]() ,当
,当![]() 时,表达式为:
时,表达式为:![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据图象中的数据即可得到A,C两地的距离;
(2)根据函数图象中的数据即可得到小明离![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(3)根据题意可以分到B地前和到B地前后两种情况进行解答.
(1)由题意和图象可得,
A,C两地相距:120+40=160千米,
故答案为:160;
(2) 当![]() 时,设路程
时,设路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式:y=kx+b,
之间的函数表达式:y=kx+b,
由图象过点![]() 可得:
可得:
![]() 得
得![]()
当![]() 时,路程
时,路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式为:
之间的函数表达式为:![]() ,
,
由于速度不变,经过B地到大C地的时间为:![]()
当![]() 时,路程
时,路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式为:
之间的函数表达式为:![]() ;
;
(3)由题意可得,![]()
当行驶时间![]() 时,汽车离
时,汽车离![]() 地的路程不超过40 km.
地的路程不超过40 km.


科目:初中数学 来源: 题型:
【题目】如图1,将1张菱形纸片ABC的(∠ADC>90°)沿对角线BD剪开,得到△ABD和△BCD.再将△BCD以D为旋转中心,按逆时针方向旋转角α,使α=∠ADB,得到如图2所示的△DB′C,连接AC、BB′,∠DAB=45°,有以下结论:①AC=BB′;②AC⊥AB;③∠CDA=90°;④BB′= ![]() AB,其中正确结论的序号是 . (把所有正确结论的序号都填在横线上)
AB,其中正确结论的序号是 . (把所有正确结论的序号都填在横线上) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象如图,则下列说法:①
的图象如图,则下列说法:①![]() ;②
;② ![]() 是方程
是方程![]() 的解;③若点
的解;③若点![]() ,
,![]() 是这个函数的图象上的两点,且
是这个函数的图象上的两点,且![]() ,则
,则![]() ;④当
;④当![]() ,函数的值
,函数的值![]() ,则
,则![]() .其中正确的个数为( )
.其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简∣a-3∣+∣a+2∣;
(3)在a的取值范围内,m是最大的整数,n是最小的整数,求(m+n)m-n的值;
(4)在a的取值范围内,当a取何整数时,不等式2ax+x>2a+1的解为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,函数
,函数![]() 与
与![]() 的图像交于第四象限的点
的图像交于第四象限的点![]() ,且点
,且点![]() 的横坐标为1.
的横坐标为1.
(1)求![]() 的值;
的值;
(2)观察图像,当![]() 满足 时,
满足 时,![]() ;
;
(3)在![]() 轴上有一点
轴上有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交函数
轴的垂线,分别交函数![]() 和
和![]() 的图像于点
的图像于点![]() .若
.若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
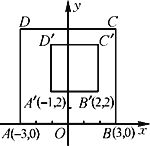
【题目】如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘同一实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
投中频率(n/m) | 0.56 | 0.60 |
| 0.49 |
|
|
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com