
【题目】如图1,将1张菱形纸片ABC的(∠ADC>90°)沿对角线BD剪开,得到△ABD和△BCD.再将△BCD以D为旋转中心,按逆时针方向旋转角α,使α=∠ADB,得到如图2所示的△DB′C,连接AC、BB′,∠DAB=45°,有以下结论:①AC=BB′;②AC⊥AB;③∠CDA=90°;④BB′= ![]() AB,其中正确结论的序号是 . (把所有正确结论的序号都填在横线上)
AB,其中正确结论的序号是 . (把所有正确结论的序号都填在横线上) 
【答案】①②③
【解析】解:如图1, 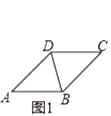
∵四边形ABCD为菱形,
∴AB=BC=CD=AD,∠A=∠C=45°,
∴∠ADB=∠ABD=67.5°,
∴α=2∠ADB=135°,
如图2,
∵将△BCD以D为旋转中心,按逆时针方向旋转角135°,
∴DB=DB′,DC=DA,CB′=AB,∠7=∠3=67.5°,∠6=135°,
在△DBB′中,∠4=∠5= ![]() (180°﹣135°)=22.5°,
(180°﹣135°)=22.5°,
∴∠ABB′=∠3+∠4=90°,∠BB′C=∠5+∠7=90°,
∴AB∥CB′,
而AB=CB′,
∴四边形ABB′C为矩形,
∴AC=BB′,AC⊥AB,所以①②正确,
∵∠CAB=90°,∠1=45°,
∴∠CAD=45°,
而DC=DA,
∴△ADC为等腰直角三角形,
∴∠CDA=90°;BB′= ![]() AB,所以③正确,④错误.
AB,所以③正确,④错误.
所以答案是①②③.
【考点精析】根据题目的已知条件,利用菱形的性质和旋转的性质的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形![]() 中,
中,![]() =4cm,
=4cm,![]() =3cm,
=3cm,![]() 为
为![]() 的中点.动点
的中点.动点![]() 从
从![]() 点出发,以每秒1cm的速度沿
点出发,以每秒1cm的速度沿![]() 运动,最终到达点
运动,最终到达点![]() .若点
.若点![]() 运动的时间为
运动的时间为![]() 秒,则当
秒,则当![]() =________ 时,
=________ 时,![]() 的面积等于4.5.
的面积等于4.5.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() .
.
(1)若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在一次函数
在一次函数![]() 的图象上,求
的图象上,求![]() 的值;
的值;
(2)求由直线![]() ,(1)中的直线
,(1)中的直线![]() 以及
以及![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
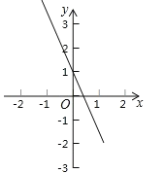
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数y= ![]() (k≠0)在第一象限内的图象经过点D、E,且cos∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且cos∠BOA= ![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和m的值;
(3)若反比例函数的图象与矩形的边BC交于点F,点G、H分别是y轴、x轴上的点,当△OGH≌△FGH时,求线段OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=18,则线段EF的长为( ) 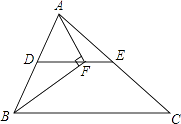
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示,折线OAB表示
之间的函数关系如图所示,折线OAB表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)甲采摘园的门票是 元,两个采摘园优惠前的草莓单价是每千克 元;
(2)当![]() >10时,求
>10时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
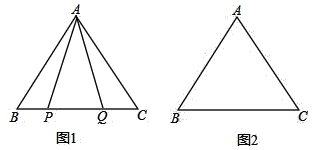
【题目】在等边△ABC中,
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;②小明通过观察、实验,提出猜想:在点P,Q运动的过程中,始终有PA=PM,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证PA=PM,只需证△APM是等边三角形.
想法2:在BA上取一点N,使得BN=BP,要证PA=PM,只需证△ANP≌△PCM.……
请你参考上面的想法,帮助小明证明PA=PM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,元旦期间,小明乘汽车从![]() 地出发,经过
地出发,经过![]() 地到目的地
地到目的地![]() 地(三地在同一条直线上),假设汽车从
地(三地在同一条直线上),假设汽车从![]() 到
到![]() 的过程都是匀速直线行驶.图②表示小明离
的过程都是匀速直线行驶.图②表示小明离![]() 地的路程
地的路程![]() (km)与汽车从
(km)与汽车从![]() 出发后行驶时间
出发后行驶时间![]() (h)之何的函数关系图像.
(h)之何的函数关系图像.
(1)![]() 两地间的路程为 km;
两地间的路程为 km;
(2)求小明离![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(3)当行驶时间![]() 在什么范围时,汽车离
在什么范围时,汽车离![]() 地的路程不超过40 km?
地的路程不超过40 km?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com