练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】(1)如图，因为直线AB、CD相交于点P，AB∥EF，所以CD不平行于EF(________________________________________________________)；

    (2)因为直线a∥b，b∥c，所以a∥c(________________________________)．

    【答案】经过直线外一点，有且只有一条直线与这条直线平行　平行于同一直线的两条直线平行

    【解析】

    （1）利用经过直线外一点，有且只有一条直线与这条直线平行，进而得出答案；

    （2）利用平行于同一直线的两条直线平行进而得出答案．

    （1）如图，因为直线AB、CD相交于点P，AB∥EF，所以CD不平于EF（经过直线外一点，有且只有一条直线与这条直线平行）；

    故答案为：经过直线外一点，有且只有一条直线与这条直线平行．

    （2）因为直线a∥b，b∥c，所以a∥c（平行于同一直线的两条直线平行）．

    故答案为：平行于同一直线的两条直线平行．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上，点O为原点，点A表示的数为a，点B表示的数为b，且a，b满足

    ，B两点对应的数分别为______，______；

    若将数轴折叠，使得A点与B点重合，则原点O与数______表示的点重合；

    若点A、B分别以4个单位秒和3个单位秒的速度相向而行，则几秒后A、B两点相距1个单位长度？

    若点A、B以中的速度同时向右运动，点P从原点O以7个单位秒的速度向右运动，是否存在常数m，使得为定值，若存在，请求出m值以及这个定值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校组织学生参观航天展览，甲、乙、丙、丁四位同学随机分成两组乘车．
    （1）哪两位同学会被分到第一组，写出所有可能；
    （2）用列表法（或树状图法）求甲、乙分在同一组的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，将1张菱形纸片ABC的（∠ADC＞90°）沿对角线BD剪开，得到△ABD和△BCD．再将△BCD以D为旋转中心，按逆时针方向旋转角α，使α=∠ADB，得到如图2所示的△DB′C，连接AC、BB′，∠DAB=45°，有以下结论：①AC=BB′；②AC⊥AB；③∠CDA=90°；④BB′= AB，其中正确结论的序号是 ． （把所有正确结论的序号都填在横线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD⊥AB于D，EF⊥AB于F．

    (1)求证：EF∥CD；

    (2)若DE∥BC，EF平分∠AED，求证：CD平分∠ACB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD的边AB=1，BE平分∠ABC，交AD于点E，若点E是AD的中点，以点B为圆心，BE为半径画弧，交BC于点F，则图中阴影部分的面积是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O．

    （1）求证：△AEC≌△BED；

    （2）若∠1=42°，求∠BDE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对任意一个三位数n，如果n满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F（n）．例如n=123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132=666，666÷111=6，所以F（123）=6．
    （1）计算：F（243），F（617）；
    （2）若s，t都是“相异数”，其中s=100x+32，t=150+y（1≤x≤9，1≤y≤9，x，y都是正整数），规定：k= ，当F（s）+F（t）=18时，求k的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

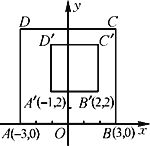
    【题目】如图，在平面直角坐标系xOy中，对正方形ABCD及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘同一实数a，将得到的点先向右平移m个单位长度，再向上平移n个单位长度(m>0，n>0)，得到正方形A′B′C′D′及其内部的点，其中点A，B的对应点分别为A′，B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合，求点F的坐标.

    查看答案和解析>>

    同步练习册答案