练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．用围棋子按下面的规律摆图形，则摆第2012个图形需要围棋子的枚数是（　　）
    A．6035B．6038C．6041D．6044

    分析 观察图形得到第1个图形需要围棋子的枚数是5，第2个图形需要围棋子的枚数是5+3，第3个图形需要围棋子的枚数是5+3×2，第4个图形需要围棋子的枚数是5+3×3，…，则第n个图形需要围棋子的枚数是5+3（n-1），然后把n=2012代入计算即可．

    解答 解：第1个图形需要围棋子的枚数=5，
    第2个图形需要围棋子的枚数=5+3，
    第3个图形需要围棋子的枚数=5+3×2，
    第4个图形需要围棋子的枚数=5+3×3，
    …，
    则第2012个图形需要围棋子的枚数是：5+3×2011=6038．
    故选B．

    点评 本题考查了图形的变化类，通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．一个球的表面积是100πcm2，则这个球的半径是（　　）（球的表面积S=4πR2，其中R是球的半径）
    A．10cmB．5cmC．±10cmD．±5cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解方程：$\sqrt{3}$-2$\sqrt{6}$x=-2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．用火柴棒搭三角形时，大家都知道，3根火柴棒只能搭成1种三角形，不妨记作它的边长分别为1，1，1；4根火柴棒不能搭成三角形；5根火柴棒只能搭成一种三角形，其边长分别为2，2，1；6根火柴棒只能搭成一种三角形，其边长分别为2，2，2；7根火柴棒只能搭成2种三角形，其边长分别为3，3，1和3，2，2；那么20根火柴棒能搭成三角形个数是9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

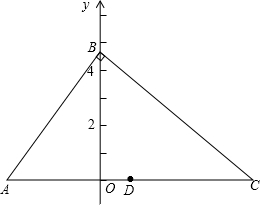    4．如图，Rt△ABC在直角坐标系中，∠ABC=90°，AB：BC：AC=3：4：5，点A的坐标为（-4，0），点C的坐标为（6，0），点B在y轴正半轴上，点D为AC的中点．
    （1）求点B的坐标；
    （2）动点P从点B出发以每秒6个单位长度的速度，沿着△OBC的三边B-O-C-B，回到B处停止运动，设运动时间为t，△PBD的面积为S，用含t的代数式表示S；
    （3）当点P在线段BO边上移动时，同时点M从点A出发沿线段AO以每秒4个单位长度的速度运动，点N从点O出发以每秒a个单位长度沿y轴负半轴运动，问：当t为何值时，以P、O、C为顶点的三角形与以M、O、N为顶点的三角形全等，并求出相应的a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，平行四边形ABCD中，AE⊥BD于E，且BE：DE=3：7，BD=20，AB=10，则AB，CD的距离为16．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．在平行四边形ABCD中，AB=2BC，M是AB的中点，求证：DM⊥CM．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．$\frac{\sqrt{5}}{2}$＞$\frac{1}{2}$．（填“＞”、“＜”或“=”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算
    （1）$\root{3}{64}$-$\sqrt{（-\frac{1}{3}）^{2}}$+$\sqrt{-（-1）^{5}}$+$\sqrt{0}$
    （2）$\frac{x-3}{3}$-$\frac{6x-1}{6}$＞-3．

    查看答案和解析>>

    同步练习册答案