
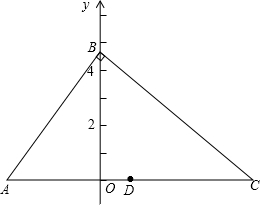
 如图,Rt△ABC在直角坐标系中,∠ABC=90°,AB:BC:AC=3:4:5,点A的坐标为(-4,0),点C的坐标为(6,0),点B在y轴正半轴上,点D为AC的中点.
如图,Rt△ABC在直角坐标系中,∠ABC=90°,AB:BC:AC=3:4:5,点A的坐标为(-4,0),点C的坐标为(6,0),点B在y轴正半轴上,点D为AC的中点.分析 (1)根据A、C的坐标求得OA=4,OC=6,根据射影定理即可求得OB,即可求得B的坐标;
(2)分三种情况讨论;根据三角形的中位线,可得DE的长,根据三角形的面积公式,可得答案;
(3)根据全等三角形的对应边相等,可得方程组,根据解方程组,可得答案.
解答 解:(1)∵点A的坐标为(-4,0),点C的坐标为(6,0),
∴OA=4,OC=6,
∴AC=10,
∵∠ABC=90°,BO⊥AC,
∴OB2=OA•OC=4×6=24,
∴OB=2$\sqrt{6}$,
∴B(0,2$\sqrt{6}$);
(2)∵点D为AC的中点.
∴DC=$\frac{1}{2}$AC=5,
∴OD=1,
如图1:作DE⊥BC于E,则DE∥AB.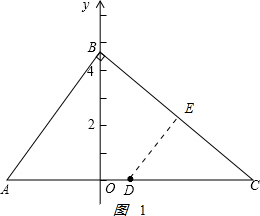 ,
,
∵点D为AC的中点.
∴DE=$\frac{1}{2}$AB,
∵AC=10,AB:BC:AC=3:4:5,
∴AB=6,BC=8,
∴DE=3,
①当P点在OB上时,S=$\frac{1}{2}$×6t×1=3t;
②当P点在OC上,且在D的左边时,S=S△BOD-S△BOP=$\frac{1}{2}$×1×2$\sqrt{6}$-$\frac{1}{2}$(6t-2$\sqrt{6}$)×2$\sqrt{6}$=-6$\sqrt{6}$t+$\sqrt{6}$+12;
③当P点在OC上,且在D的右边时,S=S△BOP-S△BOD=$\frac{1}{2}$(6t-2$\sqrt{6}$)×2$\sqrt{6}$-$\frac{1}{2}$×1×2$\sqrt{6}$=6$\sqrt{6}$t-12-$\sqrt{6}$;
④当P点在BC上时,S=$\frac{1}{2}$BP•DE=$\frac{1}{2}$(8+6+2$\sqrt{6}$-6t)×3=21+3$\sqrt{6}$-9t;
(3)如图2: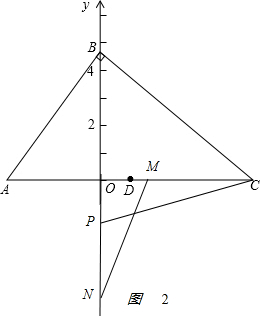 ,
,
由△POC≌△MON,得
OM=OP,ON=OC,
∴$\left\{\begin{array}{l}{4t-4=6t-2\sqrt{6}}\\{at=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{t=\sqrt{6}-2}\\{a=3\sqrt{6}+6}\end{array}\right.$,
当t=$\sqrt{6}$-2时,以P、O、C为顶点的三角形与以M、O、N为顶点的三角形全等,相应的a=3$\sqrt{6}$+6;
如图3: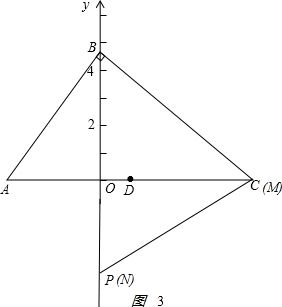 ,
,
由△POC≌△NOM,得
$\left\{\begin{array}{l}{PO=NO}\\{CO=MO}\end{array}\right.$,即$\left\{\begin{array}{l}{6t-2\sqrt{6}=at}\\{4t-4=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{t=\frac{5}{2}}\\{a=\frac{30-4\sqrt{6}}{5}}\end{array}\right.$,
当t=$\frac{5}{2}$时,以P、O、C为顶点的三角形与以M、O、N为顶点的三角形全等,相应的a=$\frac{30-4\sqrt{6}}{5}$
综上所述:当t=$\sqrt{6}$-2时,以P、O、C为顶点的三角形与以M、O、N为顶点的三角形全等,相应的a=3$\sqrt{6}$+6;
当t=$\frac{5}{2}$时,以P、O、C为顶点的三角形与以M、O、N为顶点的三角形全等,相应的a=$\frac{30-4\sqrt{6}}{5}$.
点评 本题考查了一次函数综合题,利用了射影定理,三角形的面积公式,全等三角形的性质,分类讨论是解题关键.


 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com