
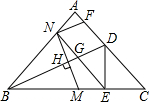
 ��ͼ���ڵ���Rt��ABC�У�AB=AC����BAC=90�㣬DΪAC��һ�㣬��BD�۵���ABC��ʹA������BC���ϵĵ�E����MΪ��BC���е㣬MN��BD���H��N��AB���ϣ�����NE��BD�ڵ�G������N��BD��ƽ���߽�AC�ڵ�F�����н��ۣ���AB=$\sqrt{2}$BN�����ı���DFNGΪƽ���ı��Σ��ۡ�BMN�ס�EDG����AN=DF��������ȷ���۵ĸ����ǣ�������
��ͼ���ڵ���Rt��ABC�У�AB=AC����BAC=90�㣬DΪAC��һ�㣬��BD�۵���ABC��ʹA������BC���ϵĵ�E����MΪ��BC���е㣬MN��BD���H��N��AB���ϣ�����NE��BD�ڵ�G������N��BD��ƽ���߽�AC�ڵ�F�����н��ۣ���AB=$\sqrt{2}$BN�����ı���DFNGΪƽ���ı��Σ��ۡ�BMN�ס�EDG����AN=DF��������ȷ���۵ĸ����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� �ٸ��������֪BA=BE��BN=BM�����ݵ���ֱ�������ε����ʽ��м��㣬�õ�����ȷ��
�ڼ����BC��BE�Ĺ�ϵ��BA��BN�Ĺ�ϵ������ƽ���ߵ��ж���֤��NE��AC���õ�����ȷ��
�۸�������ֱ��������BNM����BMN�Ķ����͡�DGE����GDE�Ķ�����֤����BMN�ס�EDG���õ�����ȷ��
�ܸ��ݽ�ƽ���ߵ�������BN��ʾNA��NG���õ���ȹ�ϵ��֤������ȷ��
��� ֤������AB=AC����BAC=90�㣬
��BC=$\sqrt{2}$AB��
��MΪBC���е㣬
��2BM=$\sqrt{2}$AB��AB=$\sqrt{2}$BM��
�ߡ�NBH=��MBH��BH��MN��
��BN=BM����AB=$\sqrt{2}$BN��
�����ȷ��
��BE=BA��
��BC=$\sqrt{2}$BE��
�֡�AB=$\sqrt{2}$BN��
��NE��AC����NF��BD��
���ı���DFNGΪƽ���ı��Σ�
�����ȷ��
��NE��AC��
���BNE=90�㣬
�ߡ�NBG=22.5�㣬
���NGB=67.5�㣬
���DGE=67.5�㣬
�ߡ�BED=90�㣬��DBE=22.5�㣬
���GDE=67.5�㣬
��BM=BN����NBM=45�㣬
���BNM=��BMN=67.5�㣬
���BMN�ס�EDG��
�����ȷ��
��BGƽ�֡�NBE��
��$\frac{BN}{BE}$=$\frac{NG}{EG}$��NG=��$\sqrt{2}-1$��NE��
AN=��$\sqrt{2}$-1��BN��
�ߡ�BNE=90�㣬��NBM=45�㣬
��NB=NE��
��NA=NG��
�֡�NG=DF��
��AN=DF��
�����ȷ��
��ѡ��D��
���� �����ۺϿ����˵���ֱ�������ε����ʡ�ƽ���ߵ��ж������������ε��ж��ͽ�ƽ���ߵ����ʣ��ۺ���ǿ���ѶȽϴ��ʱ����Ҫѧ�������ۺ�����֪ʶ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
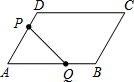 ��ͼ����ƽ���ı���ABCD�У�AB=8cm��AD=4cm����A=60�㣬����P��2cm/s���ٶȴ�D���A�ƶ�������Q��4cm/s���ٶȴӵ�A���B�ƶ������P��Q����ֱ��D��Aͬʱ��������һ�������յ�ʱ����ֹ֮ͣ�˶�����ô����1�룬�����PQBCD�����С��
��ͼ����ƽ���ı���ABCD�У�AB=8cm��AD=4cm����A=60�㣬����P��2cm/s���ٶȴ�D���A�ƶ�������Q��4cm/s���ٶȴӵ�A���B�ƶ������P��Q����ֱ��D��Aͬʱ��������һ�������յ�ʱ����ֹ֮ͣ�˶�����ô����1�룬�����PQBCD�����С���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
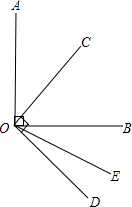 ��ͼ����AOB=��COD=90�㣬OCƽ�֡�AOB����BOE=2��DOE�������COE�Ķ�����
��ͼ����AOB=��COD=90�㣬OCƽ�֡�AOB����BOE=2��DOE�������COE�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com