
分析 两种情况:①由矩形的性质得出CD=AB=3,BC=AD=5,∠ADB=∠CDF=90°,由菱形的性质得出CF=EF=BE=BC=5,由勾股定理求出DF,得出MF,即可求出AM;②同①得出AE=4,求出ME,即可得出AM的长.
解答 解:分两种情况:①如图1所示: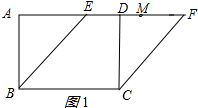 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴CD=AB=3,BC=AD=5,∠ADB=∠CDF=90°,
∵四边形BCFE为菱形,
∴CF=EF=BE=BC=5,
∴DF=$\sqrt{C{F}^{2}-C{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AF=AD+DF=9,
∵M是EF的中点,
∴MF=$\frac{1}{2}$EF=2.5,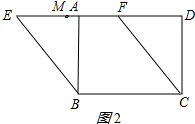 ∴AM=AF-DF=9-2.5=6.5;
∴AM=AF-DF=9-2.5=6.5;
②如图2所示:同①得:AE=4,
∵M是EF的中点,
∴ME=2.5,
∴AM=AE-ME=1.5;
综上所述:线段AM的长为:6.5,或1.5;
故答案为:6.5,或1.5.
点评 本题考查了矩形的性质、菱形的性质、勾股定理;熟练掌握矩形和菱形的性质,运用勾股定理进行计算和分类讨论是解决问题的关键.


科目:初中数学 来源: 题型:解答题
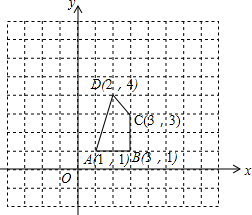 将图中的四边形作下列运动,画出相应的图形,并写出各个顶点的坐标;
将图中的四边形作下列运动,画出相应的图形,并写出各个顶点的坐标;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
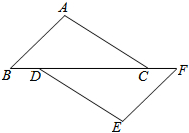 如图,点B、D、C、F在同一直线上,且BD=FC,AB=EF.请你在横线上添加一个条件:∠B=∠ACB(不再添加辅助线),使△ABC≌△EFD,并说明理由.
如图,点B、D、C、F在同一直线上,且BD=FC,AB=EF.请你在横线上添加一个条件:∠B=∠ACB(不再添加辅助线),使△ABC≌△EFD,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com