
���� ��1������B��BC��OC������ΪC���������֪��BOC=30�㣬OB=2������õ�B�����꣬Ȼ��A��O��B��������������ߵĽ���ʽ���Ӷ������a��b��c��ֵ��
��2������������ߵĶԳ���Ϊx=1�����P������Ϊ��1��a�����������ľ��빫ʽ���PO��PB�ij���Ȼ���ΪPO=PB��OB=BP��BP=BO��������з�����⼴�ɣ�
��3������D��x��Ĵ��ߣ���OB�ڵ�C�������ֱ��OB�Ľ���ʽΪy=$-\frac{\sqrt{3}}{3}$x�����D������Ϊ��a��$\frac{2\sqrt{3}-3}{3}$a2+$\frac{6-4\sqrt{3}}{3}$a�������C������Ϊ��a��-$\frac{\sqrt{3}}{3}a$�����Ӷ��ɱ�ʾ��DC�ij����������ε������ʽ����á�OBD�������a�ĺ�����ϵʽ���ɶ��κ��������ʿ���á�OBD����������ֵ��Ȼ������á�AOB��������Ӷ�������ı���AODB����������
��� �⣺��1����ͼ��ʾ������B��BC��OC������ΪC��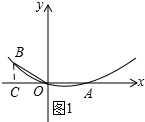
�ߡ�BOA=150�㣬OB=OA��
���BOC=30�㣬OB=2��
��BC=1��OC=$\sqrt{3}$��
���B��������-$\sqrt{3}$��1����
����0��0������2��0������-$\sqrt{3}$��1�����������ߵĽ���ʽ�ã�$\left\{\begin{array}{l}{c=0}\\{4a+2b+c=0}\\{3a-\sqrt{3}b+c=1}\end{array}\right.$��
��ã�c=0��a=$\frac{2\sqrt{3}-3}{3}$��b=$\frac{6-4\sqrt{3}}{3}$��
�������ߵĽ���ʽΪy=$\frac{2\sqrt{3}-3}{3}$x2+$\frac{6-4\sqrt{3}}{3}$x��
��2����x=-$\frac{b}{2a}$��֪��x=1��
���P��������1��a����
��OP=OBʱ���ɵ��ľ��빫ʽ��֪��12+a2=2�����a=��$\sqrt{3}$��
��a=��$\sqrt{3}$��
���P��������1��$\sqrt{3}$����1��-$\sqrt{3}$����
��PO=PBʱ���������ľ��빫ʽ��֪��12+a2=��1+$\sqrt{3}$��2+��a-1��2����ã�a=2+$\sqrt{3}$��
��a=2+$\sqrt{3}$��
���P�����꣨1��2+$\sqrt{3}$����
��PB=OBʱ��
��PB��$\sqrt{3}$+1��OB=2��
��PB��OB��
����������������
���P��������1��$\sqrt{3}$����1��-$\sqrt{3}$����1��2+$\sqrt{3}$����
��3����ͼ2��ʾ������D��x��Ĵ��ߣ���OB�ڵ�C��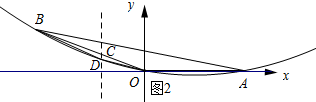
��OB�Ľ���ʽΪy=kx��
�߽���B���������ã�-$\sqrt{3}$k=1�����k=-$\frac{\sqrt{3}}{3}$��
��ֱ��OB�Ľ���ʽΪy=$-\frac{\sqrt{3}}{3}$x��
���D��������a��$\frac{2\sqrt{3}-3}{3}$a2+$\frac{6-4\sqrt{3}}{3}$a�������C��������a��-$\frac{\sqrt{3}}{3}a$����
���OBD�����=$\frac{1}{2}$��$\sqrt{3}$����$\frac{3-2\sqrt{3}}{3}$a2+$\frac{3\sqrt{3}-6}{3}$a��=$\frac{3\sqrt{3}-6}{6}{a}^{2}+\frac{9-6\sqrt{3}}{6}$a��
�൱a=$-\frac{\sqrt{3}}{2}$ʱ����OBD��������ֵ����OBD����������ֵ=$\frac{2-\sqrt{3}}{2}$��
�ߡ�AOB�����=$\frac{1}{2}��2��1$=1��
���ı���AODB��������=1+$\frac{2-\sqrt{3}}{2}$=$\frac{4-\sqrt{3}}{2}$��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ������һ�κ��������κ����Ľ���ʽ�������ľ��빫ʽ������������Ǻ���ֵ�����κ�������ֵ����á�OBD��������D�ĺ�����֮��ĺ�����ϵʽ�ǽ���Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
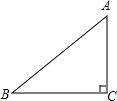 ��Rt��ABC�У���֪��C=90�㣬BC=6��cosB=$\frac{3}{4}$����AC�ij���
��Rt��ABC�У���֪��C=90�㣬BC=6��cosB=$\frac{3}{4}$����AC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 35�� | B�� | 40�� | C�� | 70�� | D�� | 110�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com