
分析 根据小数由整数部分、小数部分和小数点组成.当测量物体时往往会得到的不是整数的数,古人就发明了小数来补充整数 小数是十进制分数的一种特殊表现形式.
解答 解:-$\frac{2}{3}$,5.$\stackrel{•}{6}$,-8$\frac{1}{4}$,$\frac{1}{9}$,31.25,-3.5,20%是小数,
故答案为:-$\frac{2}{3}$,5.$\stackrel{•}{6}$,-8$\frac{1}{4}$,$\frac{1}{9}$,31.25,-3.5,20%.
点评 本题考查了有理数,小数由整数部分、小数部分和小数点组成.当测量物体时往往会得到的不是整数的数,古人就发明了小数来补充整数 小数是十进制分数的一种特殊表现形式.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B. | $\frac{-x+y}{x-y}$=-1 | C. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | D. | $\frac{x+2}{x+3}$=$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24cm和12cm | B. | 16cm和22cm | C. | 20cm和16cm | D. | 22cm和16cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
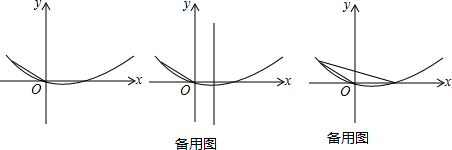
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com