
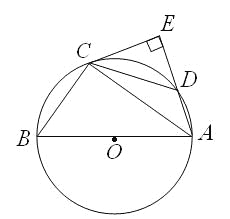
【题目】如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,点 D 为边 BC 的点,点 E、F 分别是边 AB、AC 上两点,且 EF∥BC,若 AE:EB=m,BD:DC=n,则( )
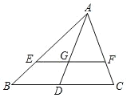
A.若 m>1,n>1,则 2S△AEF>S△ABDB.若 m>1,n<1,则 2S△AEF<S△ABD
C.若 m<1,n<1,则 2S△AEF<S△ABDD.若 m<1,n>1,则 2S△AEF<S△ABD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具用品商店销售A、B两种款式文具盒,已知购进1个A款文具盒比B款文具盒便宜5元,且用300元购入A款文具盒的数量比购入B款文具盒的数量多5个.
(1)购进一个A款文具盒、一个B款文具盒各需多少元?
(2)若A款文具盒与B款文具盒的售价分别是20元和30元,现该文具用品商店计一划用不超过1000元购入共计60个A、B两种款式的文具盒,且全部售完,问如何安排进货才能使销售利润最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
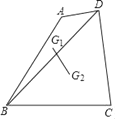
【题目】如图,BD是四边形ABCD的对角线,AB=BC=6,∠ABC=60°,点G1、G2分别是△ABD和△DBC的重心,则点G1、G2间的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
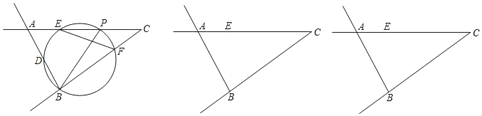
【题目】如图,在锐角△ABC中,BC=10,AC=11,△ABC的面积为33,点P是射线CA上一动点,以BP为直径作圆交线段AC于点E,交射线BA于点D,交射线CB于点F.
(1)当点P在线段AC上时,若点E为![]() 中点,求BP的长.
中点,求BP的长.
(2)连结EF,若△CEF为等腰三角形,求所有满足条件的BP值.
(3)将DE绕点D顺时针旋转90°,当点E的对应点E'恰好落在BC上时,记△DBE'的面积为S1,△DPE的面积S2,则![]() 的值为 .(直接写出答案即可)
的值为 .(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
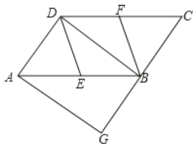
【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
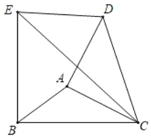
【题目】如图,分别以△ABC中BC和AC为腰向外作等腰直角△EBC和等腰直角△DAC,连结DE,且DE∥BC,EB=BC=6,四边形EBCD的面积为24,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,
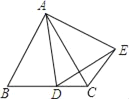
(1)求证:△ABD≌△ACE;
(2)若CE=![]() ,求△ACD的面积;
,求△ACD的面积;
(3)若△ACE是直角三角形,则BD的长是 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,有一个由六个边长为1的正方形组成的图案,其中点A,B的坐标分别为(3,5),(6,1).若过原点的直线l将这个图案分成面积相等的两部分,则直线l的函数解析式为_____.
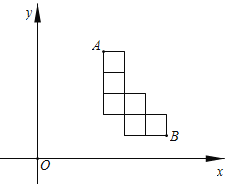
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com