
【题目】如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,
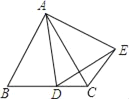
(1)求证:△ABD≌△ACE;
(2)若CE=![]() ,求△ACD的面积;
,求△ACD的面积;
(3)若△ACE是直角三角形,则BD的长是 (直接写出答案).
【答案】(1)见解析;(2)S△ACD=![]() ;(3)1或4.
;(3)1或4.
【解析】
(1)构建两边及其夹角对应相等的两个三角形全等即可证明.
(2)如图2中,作AM⊥BC于M.由(1)可知BD=CE=![]() ,求出CD、AM即可解决问题.
,求出CD、AM即可解决问题.
(3)分两种情形①如图3中,当∠AEC=90°时,②如图4中,当∠CAE=90°时,分别求解即可.
(1)证明:如图1中,
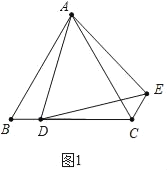
∵△ABC,△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
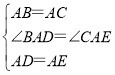 ,
,
∴△BAD≌△CAE.
(2)解:如图2中,作AM⊥BC于M.
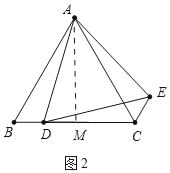
∵△ABD≌△ACE,
∴BD=CE=![]() ,∵AB=BC=2,
,∵AB=BC=2,
∴CD=BC﹣BD=![]() ,
,
在Rt△ABM中,∵∠AMB=90°,∠BAM=30°,AB=2,
∴AM=ABcos30=![]() ,
,
∴S△ACD=![]() CDAM=
CDAM=![]() ×
×![]() ×
×![]() =
=![]() .
.
(3)解:如图3中,当∠AEC=90°时,
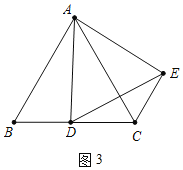
∵△ABD≌△ACE,
∴∠B=∠ACE=60°,
∴∠CAE=90°﹣∠ACE=30°,
∴EC=BD=![]() AC=1.
AC=1.
如图4中,当∠CAE=90°时,
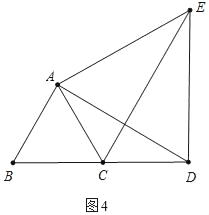
∵△ABD≌△ACE,
∴∠B=∠ACE=60
∴∠CEA=90°﹣∠ACE=30°,
∴EC=2AC=4,
∴BD=CE=4.
综上所述,BD=1或4时,△ACE是直角三角形.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
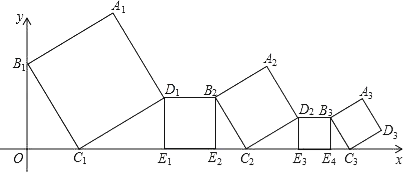
【题目】一组正方形按如图所示放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则正方形A2019B2019C2019D2019的边长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
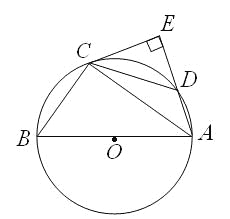
【题目】如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
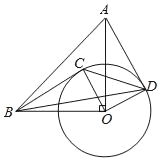
【题目】如图,在Rt△OAB中,∠AOB=90°,OA=OB=4,以点O为圆心、2为半径画圆,点C是⊙O上任意一点,连接BC,OC.将OC绕点O按顺时针方向旋转90°,交⊙O于点D,连接AD.
(1)当AD与⊙O相切时,
①求证:BC是⊙O的切线;
②求点C到OB的距离.
(2)连接BD,CD,当△BCD的面积最大时,点B到CD的距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3.
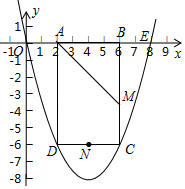
(1)求抛物线的解析式;
(2)F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;
(3)在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为![]() ?若存在,求出点P的坐标;若不存在,请说明理由;
?若存在,求出点P的坐标;若不存在,请说明理由;
(4)矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL平分矩形的面积时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在⊙0上,点P是⊙0外一点.PA切⊙0于点A.连接OP交⊙0于点D,作AB⊥OP于点C,交⊙0于点B,连接PB.
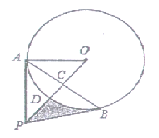
(1)求证:PB是⊙0的切线;
(2)若PC=9,AB=6![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com