
【题目】如图,点A在⊙0上,点P是⊙0外一点.PA切⊙0于点A.连接OP交⊙0于点D,作AB⊥OP于点C,交⊙0于点B,连接PB.
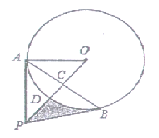
(1)求证:PB是⊙0的切线;
(2)若PC=9,AB=6![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)先证明△AOP≌△BOP,由PA切⊙O于点A得∠PAO=90°,所以∠PBO=∠PAO=90°,可得结论;
(2)先根据垂径定理得:BC=![]() ,然后证明△PBC∽△BOC,根据对应边成比例求出OC=3,再利用勾股定理求圆的半径OB的长,利用三角函数得∠COB=60°,利用三角形的面积公式和扇形的面积公式分别求S△OPB和S扇形BOD的值,最后利用面积差得结论;
,然后证明△PBC∽△BOC,根据对应边成比例求出OC=3,再利用勾股定理求圆的半径OB的长,利用三角函数得∠COB=60°,利用三角形的面积公式和扇形的面积公式分别求S△OPB和S扇形BOD的值,最后利用面积差得结论;
解:(1)证明:如图1,连接OB,
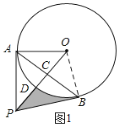
∵OA=OB,OP⊥AB,
∴AC=BC,∠AOC=∠BOC
∴OP垂直平分AB,
∵OA=OB,∠AOC=∠BOC,OP=OP,
∴△AOP≌△BOP(SAS),
∴∠PAO=∠PBO,
∵PA切⊙O于点A,
∴AP⊥OA,即∠PAO=90°,
∴∠PBO=∠PAO=90°,
∴OB⊥BP,
又∵点B在⊙O上,
∴PB是⊙O的切线.
(2)∵OP⊥AB,OP经过圆心O,∴![]()
∵∠PBO=∠BCO=90°,∴∠PBC+∠OBC=∠OBC+∠BOC=90°,
∴∠PBC=∠BOC,
∴△PBC∽△BOC,
∴![]() ,即
,即![]()
∴OC=3,
∴在Rt△OCB中,OB=![]() ,
,
tan∠BOC=![]()
∴∠COB=60°,
∴S△OPB =![]() ,S扇形BOD =
,S扇形BOD =![]() ,
,
∴S阴影=S△OPB-S扇形BOD=![]()


科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,
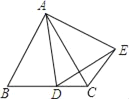
(1)求证:△ABD≌△ACE;
(2)若CE=![]() ,求△ACD的面积;
,求△ACD的面积;
(3)若△ACE是直角三角形,则BD的长是 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,有一个由六个边长为1的正方形组成的图案,其中点A,B的坐标分别为(3,5),(6,1).若过原点的直线l将这个图案分成面积相等的两部分,则直线l的函数解析式为_____.
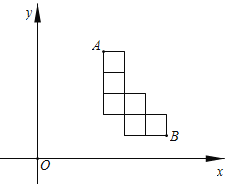
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
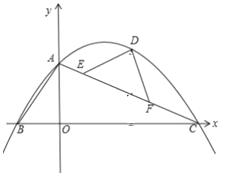
【题目】如图,平面直角坐标系中,O为坐标原点,直线y=﹣![]() x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=
x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=![]() .
.
(1)求抛物线的解析式;
(2)已知E、F是线段AC上异于A、C的两个点,且AE<AF,EF=2![]() ,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
(3)在(2)的条件下,当∠EDF=90°时,连接BD,P为抛物线上一动点,过P作PQ⊥BD交线段BD于点Q,连接EQ.设点P的横坐标为t,求t为何值时,PE=QE.
查看答案和解析>>
科目:初中数学 来源: 题型:
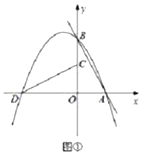
【题目】如图①,定义:直线![]() 与x、y轴分别相交于A、B两点,将
与x、y轴分别相交于A、B两点,将![]() 绕着点O逆时针旋转90°得到
绕着点O逆时针旋转90°得到![]() ,过点A、B、D的抛物线P叫做直线
,过点A、B、D的抛物线P叫做直线![]() 的“纠缠抛物线”,反之,直线
的“纠缠抛物线”,反之,直线![]() 叫做P的“纠缠直线",两线“互为纠缠线”.
叫做P的“纠缠直线",两线“互为纠缠线”.
(1)若![]() ,则纠缠物线P的函数解析式是____________.
,则纠缠物线P的函数解析式是____________.
(2)判断并说明![]() 与
与![]() 是否“互为纠缠线”.
是否“互为纠缠线”.
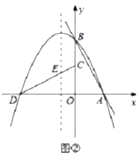
(3)如图②,若纠缠直线![]() ,纠缠抛物线P的对称轴与
,纠缠抛物线P的对称轴与![]() 相交于点E,点F在
相交于点E,点F在![]() 上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以
上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以![]() 为一边的平行四边形时,求点Q的坐标.
为一边的平行四边形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
n | 3 | 4 | 5 | 6 |
m | 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(只需把结果填在表②中)
n | 7 | 8 | 9 | 10 |
m |
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
n | 4k﹣1 | 4k | 4k+1 | 4k+2 |
m |
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了 根木棒.(只填结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com