
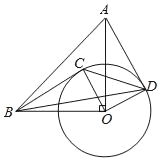
【题目】如图,在Rt△OAB中,∠AOB=90°,OA=OB=4,以点O为圆心、2为半径画圆,点C是⊙O上任意一点,连接BC,OC.将OC绕点O按顺时针方向旋转90°,交⊙O于点D,连接AD.
(1)当AD与⊙O相切时,
①求证:BC是⊙O的切线;
②求点C到OB的距离.
(2)连接BD,CD,当△BCD的面积最大时,点B到CD的距离为 .
【答案】(1)①证明见解析;②点C到OB的距离是![]() .(2)4+
.(2)4+![]() .
.
【解析】
(1)①先证明△BOC≌△AOD,则∠BCO=∠ADO=90°,BC是⊙O的切线;
②过点C作CE⊥OB,根据勾股定理得BC=2![]() ,由△BCO的面积公式可得OBCE=BCOC,求得CE=
,由△BCO的面积公式可得OBCE=BCOC,求得CE=![]() ;
;
(2)当点C在⊙O上运动到△BCD是等腰三角形,且BO的延长线与CD垂直位置时,△BCD的面积最大(如图2),由等腰直角三角形的性质可求得OF=![]() ,则点B到CD的距离为4+
,则点B到CD的距离为4+![]() .
.
(1)①证明:∵AD与⊙O相切,
∴∠ADO=90°,
∵∠AOB=∠COD=90°,
∴∠AOB﹣∠AOC=∠COD﹣∠AOC,即∠COB=∠AOD,
∵OB=OA,OC=OD,
∴△BOC≌△AOD(SAS).
∴∠BCO=∠ADO=90°.
∴BC是⊙O的切线;
②如图:
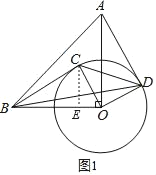
过点C作CE⊥OB,垂足为E,则CE即为点C到OB的距离,
在Rt△BOC中,∵OB=4,OC=2,
∴BC=![]() ,
,
∴OBCE=BCOC,即4CE=2×2![]() ,CE=
,CE=![]() .
.
∴点C到OB的距离是![]() ;
;
(2)当点C在⊙O上运动到△BCD是等腰三角形,且BO的延长线与CD垂直位置时,
△BCD的面积最大(如图2),
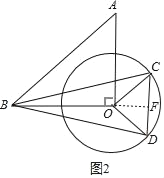
此时OB=4,OC=OD=2,
∵△COD是等腰直角三角形,
∴![]() ,
,
∴![]() .
.
故答案为:4+![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】某校初三(3)班的同学踊跃为“雅安芦山地震”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但生活委员不小心把墨水滴在统计表上,部分数据看不清楚。
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?


查看答案和解析>>
科目:初中数学 来源: 题型:
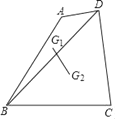
【题目】如图,BD是四边形ABCD的对角线,AB=BC=6,∠ABC=60°,点G1、G2分别是△ABD和△DBC的重心,则点G1、G2间的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
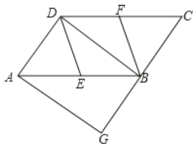
【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC中BC和AC为腰向外作等腰直角△EBC和等腰直角△DAC,连结DE,且DE∥BC,EB=BC=6,四边形EBCD的面积为24,则AB的长为_____.
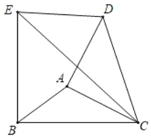
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,
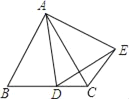
(1)求证:△ABD≌△ACE;
(2)若CE=![]() ,求△ACD的面积;
,求△ACD的面积;
(3)若△ACE是直角三角形,则BD的长是 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据《中国教育报》2004年5月24日报道:目前全国有近3万所中小学建设了校园网,该报为了了解这近3万所中小学校园网的建设情况,从中抽取了4600所学校,对这些学校校园网的建设情况进行问卷调查,并根据答卷绘制了如图的两个统计图:
说明:统计图1的百分数=![]() ×100%;
×100%;
统计图2的百分数=![]() ×100%.
×100%.
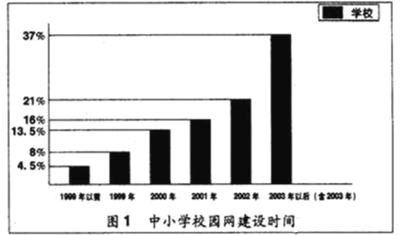
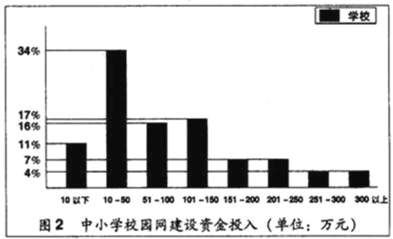
根据上面的文字和统计图提供的信息回答下列问题:
(1)在这个问题中,总体指什么?样本容量是什么?
(2)估计:在全国已建设校园网的中小学中:
①校园网建设时间在2003年以后(含2003年)的学校大约有多少所?
②校园网建设资金投入在200万元以上(不含200万元)的学校大约有多少所?
(3)所抽取的4600所学校中,校园网建设资金投入的中位数落在那个资金段内?
(4)图中还提供了其他信息,例如:校园网建设资金投入在10~50万元的中小学的数量最多等,请再写出其他两条信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com